1.
Le premier producteur fournit 70% de l'approvisionnement. Donc
p(F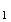 )
=0,7
)
=0,7
De plus l'usine étant approvisionné par trois producteurs on a :
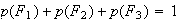
Or
le deuxième et troisième producteur se partage le reste de
l'approvisionnement de manière égale. Donc
p(F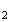 )=p(F
)=p(F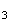 )
)
D'où:
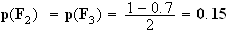
2. Probalité que la pomme prélevée soit hors calibre sachant qu'elle provient du premier producteur :
20 % des pommes fournies par le premier producteur sont hors calibre.
Donc :
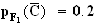
Probalité que la pomme prélevée soit de bon calibre sachant qu'elle provient du premier producteur :
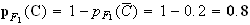
Probalité que la pomme prélevée soit hors calibre sachant qu'elle provient du deuxième producteur :
5 % des pommes fournies par le deuxième producteur sont hors calibre.
Donc :
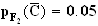
Probalité que la pomme prélevée soit de bon calibre sachant qu'elle provient du deuxième producteur :
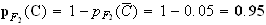
Probalité que la pomme prélevée soit hors calibre sachant qu'elle provient du troisième producteur :
4 % des pommes fournies par le troisème producteur sont hors calibre.
Donc :
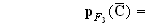 0.04
0.04
Probabilité que la pomme prélevée soit de bon calibre sachant qu'elle provient du troisième producteur :
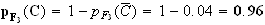
Arbre :
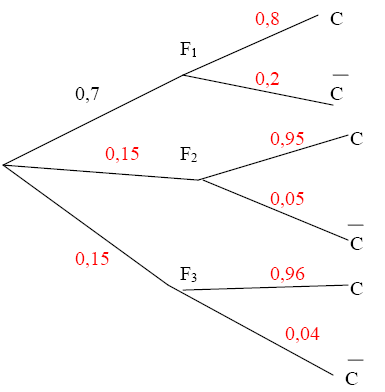
3.
On cherche la probalité telle que la pomme prélevée ait le bon
calibre et provienne du troisième producteur . Ce qui revient à
chercher
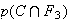
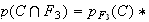
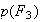
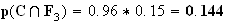
4. Calcul
de la probalité de l'évènement C :
Calcul
de la probalité de l'évènement C :
L'usine d'emballage de pommes est approvisionnée par les trois producteurs.
F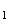 ,
F
,
F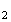 et
F
et
F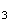 forment une partition de l'ensemble des événements
élémentaires de l'expérience aléatoire alors d'après
la formule des probabilités totales :
forment une partition de l'ensemble des événements
élémentaires de l'expérience aléatoire alors d'après
la formule des probabilités totales :
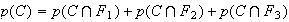
Or:
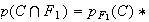
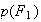
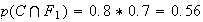
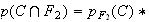
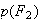
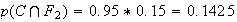
D'où :
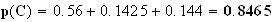
5.
Pour justifier l'affirmation du contrôleur , il faut calculer la
probabilité de
F sachant
sachant
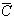 :
:
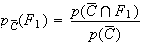
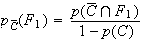
Or :
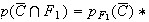
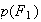
D'où:
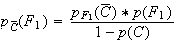
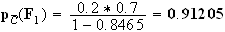
Il y a donc plus de 91% des pommes hors calibres qui proviennent du premier producteur.
L'affirmation du contrôleur est donc justifié.

