1.
La limite de la fonction f en
+
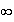est
4 car la droite d'équation y=4 est asymptote de f en
.
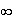2. f '(0) = 0 car le coefficient de la tangente à C passant par A est nul.
3.L'équation de la tangente à la courbe au point A est :
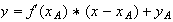
Or A pour coordonnées :
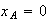
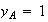
De plus :
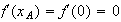d'après la question 2
Donc :
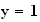
4. Lorsque on trace la fonction y = x sur le graphique , on s'aperçoit qu'elle coupe une fois la courbe C représentative de f pour un x compris en 1 et 2
Donc
sur l'intervalle ]-3;
+
[,
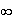l'équation f(x) = x admet une solution unique appartenant à
l'intervalle ]1; 2[.
5. Si x=0 alors f(x) = f(0)= 1 et g(x) = ln(f(x)) = ln(1) = 0
6.
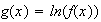
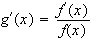car f(x) est différent de 0
Le signe de g'(x) dépend donc uniquement du signe de f'(x)
Donc
sur l'intervalle ]-3;
+
[,
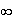g a les mêmes variations que la fonction f .
