Partie A :
1.
Calculer
u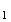
revient à calculer le nombre d'habitant de la ville au premier janvier
2006.
On
sait que population augmente de 5% par an due aux naissances et aux
décés. Cette augmentation se chiffre à :
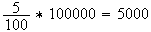
A cette augmentation il faut rajouter la population initiale de 100 000 habitants et les flux migratoires de 4000 personnes.
Ainsi :
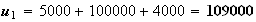
De même :
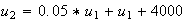
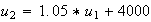
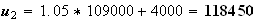
2.Soit
u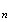
le nombre d'habitants de la ville au 1er janvier de l'année 2005 +
n.Chaque année, la balance entre les décés et les naissances
augmentent de 5%. Cette augmentation, ajouté à la
population
exixsatnte correspond aux
(1+0,05)u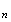
soit 1,05
u
.de
la modélisation . Il faut ajouter à cela les 4 000 personnes
supplémentaires qui viennent s'installer chaque année.
Ainsi on peut modéliser le nombre d'habitants par la formule suivante :
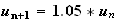
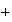
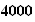
3.a)
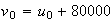
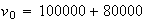
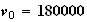
b)
v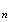
est de la forme :
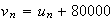
Calculons
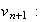
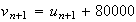
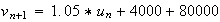
Or
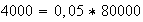
Donc :
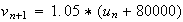
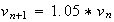
Donc
la suite
(
)
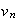est une suite géométrique de raison 1,05 et de premier terme
v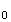
=180000.
c)
La
suite
(
)
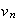est une suite géométrique de raison 1,05 et de premier terme
v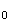
:
Donc
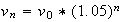
De plus :
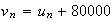
D'où :
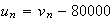
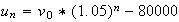
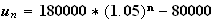
d)
limite de un en
+
:
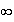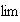
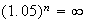car
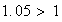
donc
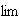
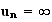
Partie B :
1.
Le nombre d'habitants de la ville au 1er janvier 2020 est donnée
par
u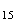
.
Or d'aprés la question 3c) de la partie A, on a :
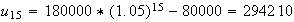
La ville aura donc 294 210 habitants en 2020.
2.
Pour savoir à partir de quelle année, la population
dépassera les 200 000 habitants, on cherche le plus
petit entier naturel n tel que
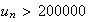
Soit:
.
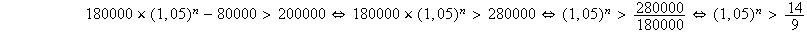1,05
et
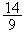sont deux réels strictement positifs et la fonction ln est strictement
croissante sur ] 0; + ∞[.
Donc
n est le plus petit entier tel que:
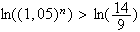
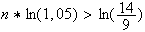
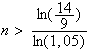
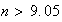
La population dépassera donc les 200000 habitants à partir de 2015.
