Pour tout x > 0 :
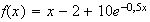
1.
limite de f en
+
:
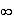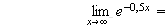
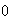car
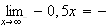
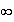et
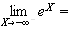
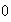
de plus :
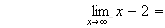
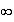
donc :
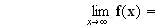
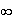
2.a)
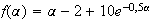
Or
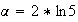
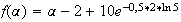
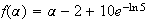
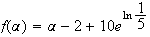
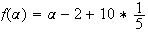
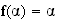
b)
La calculatrice nous permet de nous donner une valeur approchée
de
:
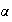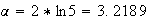
En
arrondissant au dixième, on trouve
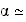
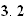
3)a)
dérivée de f pour tout x
:
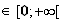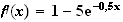
b) Etude du signe de f'(x) :
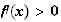
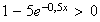
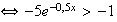
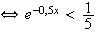
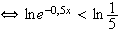car la fonction ln est strictement croissante sur
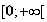
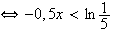
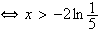
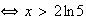
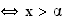
De même :
'
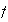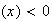
Tableau de variation de f :
____________________________________________
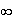
x0
+
____________________________________________
0
____________________________________________
+
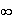
4)
Montrons que
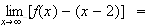
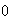
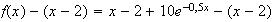
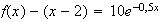
Or
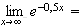
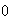
Donc :
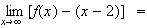
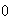
Pour
tout réel x ,
,
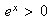donc pour tout réel x ,
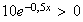
Donc :
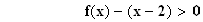
Interprétation
graphique : La droite D d'équation y=x-2 est asymptote à C (courbe
représentative de f) en
+
et la courbe (C) est au dessus de la droite
(D) en chacun de ses points.
5)a)
D'après la question 2)a), f(α)=α .
Par conséquent α est l'abscisse du point M intersection de la courbe (C) avec la droite d'équation y = x
b)
On
a vu à la question 3) que
f'(2ln5)=f'(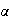
)=0
,
La tangente à la courbe (C) au point d'abscisse α a donc pour équation y = α.
Elle est représenté en rouge sur le graphique
c)
La droite D est représentée en bleu sur le graphique
Graphique :
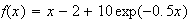
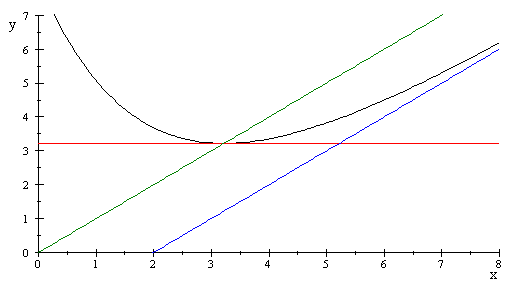
6.a) L'aire A (en unités d'aire) est l'aire du domaine E délimité par la courbe (C), la droite (D) et les droites d'équations respectives x = 2 et x = 6.
De plus d'aprés la question 4, la courbe (C) est au dessus de la droite (D) en chacun de ses points.
Donc :
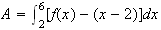
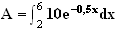
b) Valeur exacte de A :
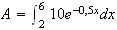
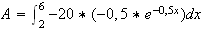
Or
une primitive de la fonction
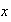
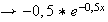est
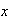
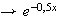(primitive de
).
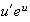Donc
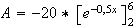
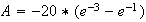
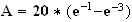
Valeur approchée au dixième de A :
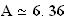(unités d'aire)
