1.
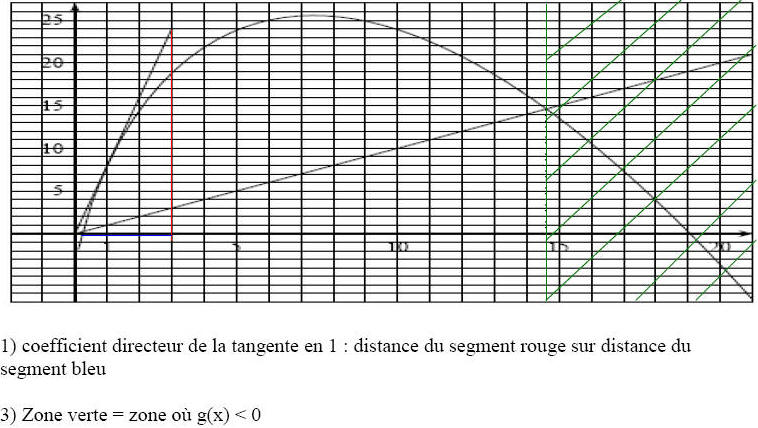
Graphiquement, on trouve g(1) = 8
g'(1)
représente le coefficient directeur de la tangente à la courbe
représentative de g. Sur le graphique, on calcule le coeeficient
directeur et on trouve
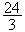 (
(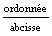 )
soit 8
)
soit 8
Donc g'(1)=8
2. Résolution
graphique de l'inéquation g(x)
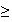 0
:
0
:
On
constate que la courbe représentative de g est au dessus de l'axe des
absices pour 0
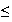 x
x
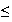 19
19
Donc
g(x)
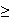 0
0
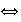 0
0
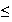 x
x
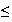 19
19
Résolution
graphique de l'inéquation g'(x)
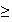 0
:
0
:
On
constate graphiquement que g est croissante pour 0
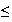 x
x
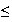 7,4 et est décroissante pour x
7,4 et est décroissante pour x
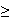 7,4
7,4
Donc
g'(x)
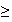 0
0
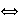 0
0
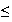 x
x
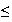 7,4
7,4
Résolution
graphique de l'inéquation g(x)
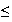 x
:
x
:
On
remarque sur le graphique que la courbe représentative de g passe en
dessous de la droite y=x dés que x
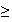 14,5
14,5
Donc
g(x)
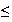 x
x
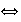 x
x
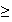 14,5
14,5
3.a)
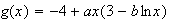
Calcul de la dérivée de g :
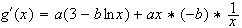 (cf produit de 2 fonctions dérivables)
(cf produit de 2 fonctions dérivables)
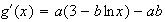
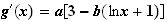
b) Dertimination des coefficients a et b :
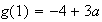
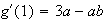 (d'aprés l'expression de
(d'aprés l'expression de
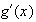 trouvée en 3a))
trouvée en 3a))
Or, d'aprés la question 1) , g(1) = 8 et g'(1) = 8
d'où le système suivant à deux équations avec 2 inconnus a et b :
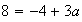
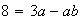
d'où :
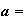
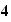
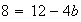
b = 1

