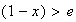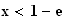1. Si B est l'évènement contraire de A, alors p(A) = 1 - p(B) .
2.
Si A et B sont deux évènements indépendants et p(A)
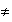 0 , alors
p
0 , alors
p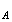 (B)
= p(B) .
(B)
= p(B) .
3.
Si A et B sont deux évènements incompatibles alors
p(A
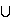 B)
= p(A) + p(B)
B)
= p(A) + p(B)
4.
Soit
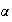 un nombre réel strictement positif ,
un nombre réel strictement positif ,
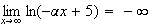
Car
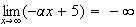
et
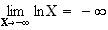
5. La représentation graphique de la fonction logarithme népérien admet une asymptote verticale d'équation x=0
6.
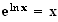 pour tout x
pour tout x
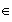 ]0,+
]0,+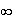 [
[
7.
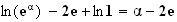
8. Soient a et b des réels strictement positifs
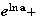
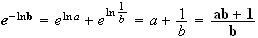
9.Une
primitive de la fonction logarithme népérien sur
]0,+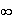 [
est xlnx - x + 3.
[
est xlnx - x + 3.
Car
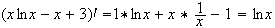
10.
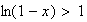
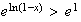 car la fonction exponentielle est croissante sur
]0,+
car la fonction exponentielle est croissante sur
]0,+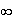 [
[