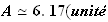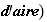1.a) Montrons tout d'abord que le point Q appartient à la droite D :
Q de
coordonnée
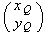appartient à la droite D SSI
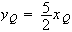
Or :
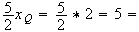
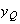
Donc le point Q appartient à la droite D.
Montrons
maintenant que Q appartient à la courbe
:
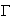Q de
coordonnée
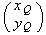appartient à la courbe
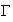SSI
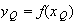
Or :
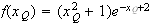
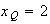
Donc :
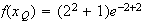
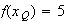
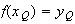
Donc le
point Q appartient à la courbe
.
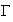Montrons
enfin que la courbe
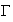coupe l'axe des ordonnées en R :
La
courbe
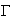coupe l'axe des ordonnées en un point M de coordonnée
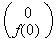
Ainsi :
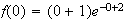
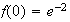
Donc M=R
Donc
la courbe
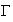coupe
l'axe des ordonnées en R.
b) Calcul de l'aire du triangle OPQ :
Soit
M le point de coordonée
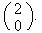
L'aire du triangle OPQ correspond à la moitié de l'aire du rectangle OPQM.(voir graphique)
Or l'aire du rectangle OPQM est OP*QM soit 5*2 soit 10 (unités d'aire )
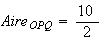
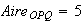(unités d'aire)
Calcul de l'aire du triangle OQR :
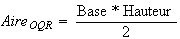
Ici base = OR et hauteur =PQ
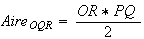
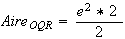
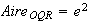(unités d'aire)
On remarque que :
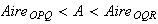
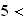
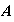
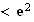
2.a)
L'aire A est l'aire du domaine délimité par la courbe
,
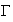la droite D et la droite d'équation x=0.
De
plus
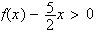(en effet graphiquement on constate que pour tout x<2 courbe
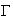au dessus de la droite D)
Donc:
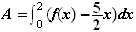
b) Calcul de la dérivée de G :
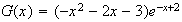
En utilisant la dérivée d'un produit de fonctions, la dérivée de G s'écrit :
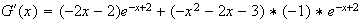
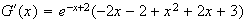
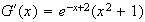
On remarque que G'(x)=f(x)
On peut en déduire que une primitive de f est G.
c)
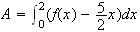
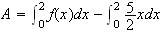
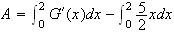
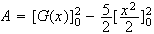
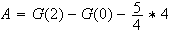
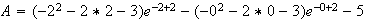
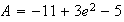
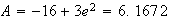
Si on arrodie au centième , une aire approchée est :
