1)a) Soit A l'évènement suivant : le ballon est crevé.
On
a donc
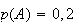 .
.
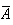 est donc l'évènement le ballon est intact.
est donc l'évènement le ballon est intact.
Les
tirs étant indépendants, la probalité telle que le
ballon soit intact au bout de 2 tirs est donc
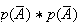 c'est à dire
c'est à dire
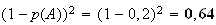
b) Pour calculer la probabilité que deux tirs suffisent pour crever le ballon , on calcule d'abord sa probalité contraire c'est à dire la probilité telle que le ballon ne soit pas crevé au bout de tirs.
C'est à dire la probalité telle que le ballon soit intact au bout de 2 tirs (0,64).(cf question précédente)
La
probalité cherché est
donc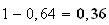
c)
Pour calculer la probalité
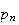 que
que
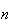 tirs suffisent pour crever le ballon., on calcule sa probalité contraire
ie la probalité telle que le ballon n'est pas crevé au bout de
tirs suffisent pour crever le ballon., on calcule sa probalité contraire
ie la probalité telle que le ballon n'est pas crevé au bout de
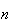 tirs.
tirs.
Cette
probalité vaut
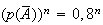 (car les tirs sont indépendants).
(car les tirs sont indépendants).
Ainsi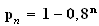
d)
On cherche les valeurs de n tels que
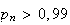
D'après la question précédente, cela équivaut à chercher les n tels que :
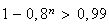
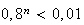
ln(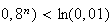 car la fonction ln est croissante.
car la fonction ln est croissante.
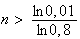
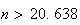
soit
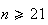
Il
faut donc que
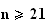 pour que
pour que
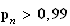
2)
Pour chaque valeur de
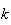 compris entre 1 et 4, la probabilité de crever le ballon est la
probabilité
compris entre 1 et 4, la probabilité de crever le ballon est la
probabilité
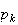 ,
:
,
:
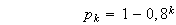 .
(d'après la question 1)c))
.
(d'après la question 1)c))
Le
dé n'est pas pipé donc chaque face a la même probabilité
de sortie égale à
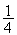 .
.
La
probabilité de crever le ballon est donc :
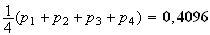
3)a)
Pour la face
n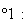
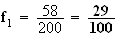
Pour
la face
n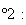
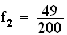
Pour
la face
n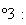
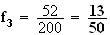
Pour
la face
n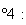
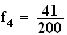
b)
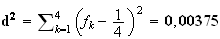
c)
On constate que
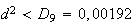
Donc, au risque de 10%, on peut considérer que le dé n'est pas pipé 7.

