1) VRAI
L'
équation
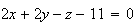est bien l'équation d'un plan
De
plus le point A vérifie cette équation
(
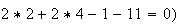
De
même le point B vérifie cette équation (
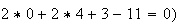
De
même le point C vérifie cette équation
(
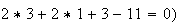
De plus les point A,B, et C sont distints entre eux.
Donc
les points A, B, C forment un plan d'équation
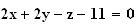
2) FAUX
Le
vecteur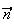 
de coordonée (2,2,-1) est un vecteur orthogonal au plan ABC.
Donc
pour que E soit le projeté orthogonal de D sur le plan ABC, il faut que
le
vecteur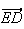
soit colinéaire au vecteur
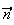et
E 
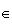(ABC)
On
a bien
E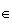 
(ABC) mais
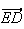n'est pas colinéaire au vecteur
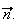
En
effet,
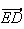a pour coordonée
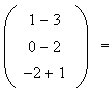
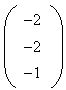qui n'est pas colinéaire à
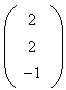
Donc E n'est pas le projeté orthogonal de D sur le plan ABC.
3) VRAI
Les
droites (AB) et
(CD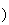
sont orthogonales
SSI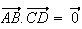 
Or
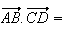
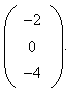
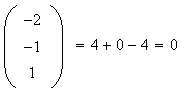
Donc
les droites (AB) et
(CD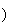
sont orthogonales.
4) FAUX
Le point D a pour coordonée (1,0,-2)
Pour que l'équation paramétrique soit celle de (CD) il faut qu'il existe au moins un réel t tel que:
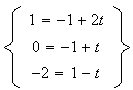
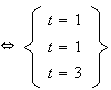
impossible
Donc
l'équation paramétrique
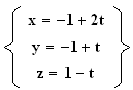n'est pas celle de la droite
(CD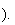
5) VRAI
Pour
montrer que I est sur la droite (AB), il suffit de montrer que
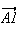et
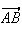sont colinéaires.
Le
vecteur
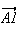a pour coordonée
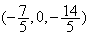
Le
vecteur
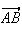a pour coordonée
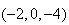
On
remarque que
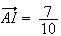
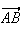
Donc
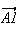et
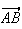sont colinéaires.
Donc I est sur la droite (AB).
