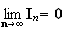1)a)
limite de f en
-
:
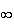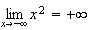
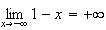
Or
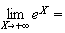
Donc
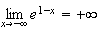
D'où
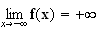
limite
de f en
+
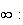
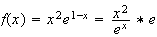
Par
croissance comparée,
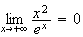
Donc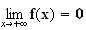
La
droite des abssices est donc asymptote à f en
+
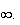
b)
f est le produit de 2 fonctions dérivables sur
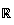donc elle est dérivable sur
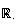et
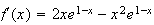
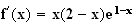
c)
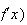est du signe de
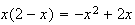qui est un polynome du second degrée. Son signe est donc celui de a ici
-1 ie négatif à l'extérieur des racines 0 et 2.
D'où le tableau de variation de f :
____________________________________________
x -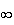
02 +
____________________________________________
_+_
____________________________________________
+
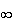
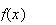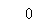
0
Graphe de f :
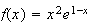
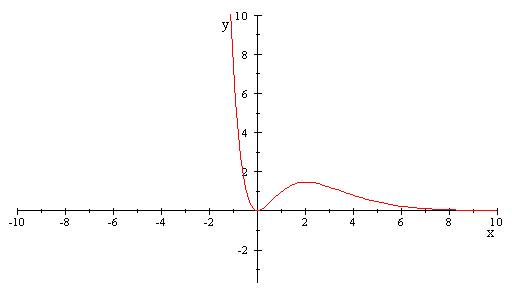
2)a)
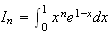
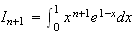
On fait une intégration par partie :
On pose :
;
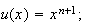
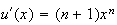
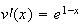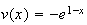
D'où :
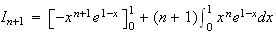
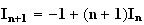
b)
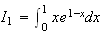
On fait une IPP:
On pose :
;
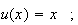
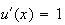
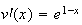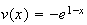
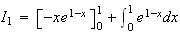
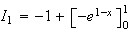
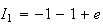
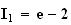
Pour
calculer
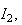on
utilise la relation calculée à la question précédente pour
n=1 :
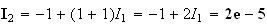
c)
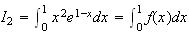
Donc
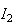représente l'aire délimitée par la courbe représentative
de f, les droites d'équations x=0 et x=1 et l'axe des abcisses.
3)a)
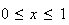
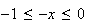
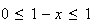
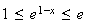car la fonction exponentielle est une fonction croissante
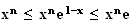car
x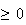
b) On passe à l'intégrale dans la relation précédente :
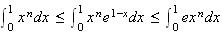
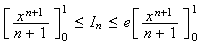
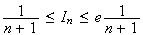
Or
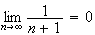et
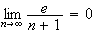
Donc en passant à la limite dans l'inégalité précédente et d'aprés le théorème des gendarmes, on obtient :
