1) a) Soit z et z' deux nombres complexes non nuls. On a :
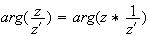
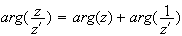 d'après le pré requis 1
d'après le pré requis 1
0r
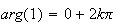
Donc d'après le pré requis 2, on a :
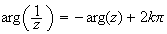
Ainsi, on a :
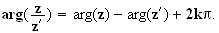
b)
Soient A, B et C trois points du plan, deux à deux distincts,
d'affixes respectives
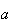 ,
,
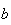 et
et
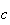 .
.
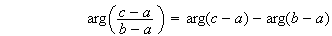
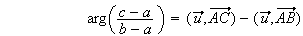 (d'après le pré requis)
(d'après le pré requis)
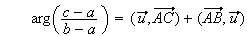
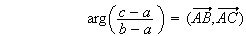 (d'après la relation de Chasles).
(d'après la relation de Chasles).
2)a)
Pour tout
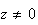 ,
on a :
,
on a :
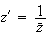
En passant aux arguments, on obtient :
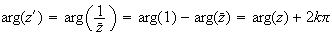 car
car
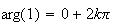 et
et
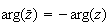
On peut donc en déduire que :
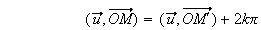
Donc
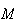 et
et
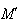 appartiennent à une même demi-droite d'origine
appartiennent à une même demi-droite d'origine
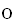 .
.
b)
On cherche l'ensemble des points M tels que
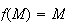 ce qui revient à chercher les
ce qui revient à chercher les
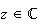 tel que :
tel que :
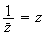
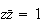
c'est-à-dire
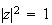
donc
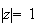 .
.
L'ensemble
des points M tels que
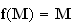 est donc le cercle de centre
est donc le cercle de centre
 et de rayon 1.
et de rayon 1.
c)
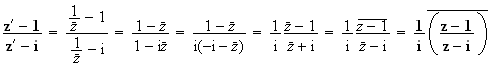
En passant à l'argument dans l'expression précédente, on obtient :
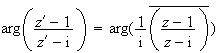
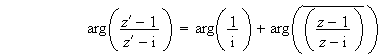
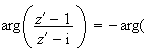 i
i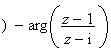
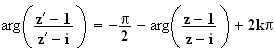 .
.
3)a)
Soit M d'affixe
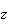 tel que
tel que
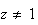 et
et
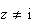 .
.
Donc
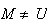 et
et
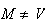
 M
appartient à la droite
M
appartient à la droite
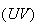 privée de
privée de
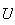 et
et
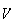
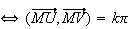
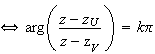
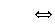
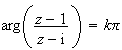
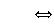
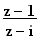 est
un nombre réel non nul.
est
un nombre réel non nul.
b)
D'aprés la question précédente
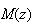 est un point de la droite
est un point de la droite
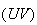 privée de
privée de
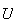 et
et
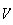 si et seulement si
si et seulement si
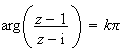
Or
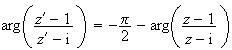 (d'après la question 2c).
(d'après la question 2c).
Donc
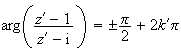
 avec
k'
avec
k'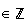
c'est-à-dire
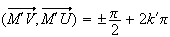 .
.
 Donc
Donc
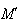 décrit le cercle de diamètre
décrit le cercle de diamètre
![$[UV]$](graphics/JG37ABJB.png) ,
privé des points
,
privé des points
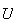 ,
,
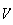 et
et
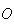 .
.
Donc
l'image par f de la droite (UV) privée de U et de V est le cercle de
diamètre
![$[UV]$](graphics/JG37ABJJ.png) ,
privé des points
,
privé des points
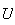 ,
,
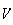 et
et
 .
.

