CORRIGE de Mathématiques-Informatique
France Métropolitaine - Section S - Juin 2006
1) Variation de g :
La
fonction
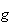 est dérivable car elle est la somme de fonctions dérivables.
est dérivable car elle est la somme de fonctions dérivables.
et
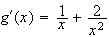
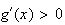 car
car
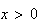
Donc
g est strictement croissante sur
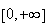
Limites de g :
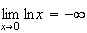 et
et
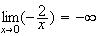 donc
donc
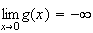
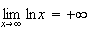 et
et
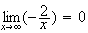 donc
donc
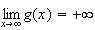
Justification
de l'existence de
x
La
fonction
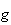 est continue sur
est continue sur
![$[2,3~;~2,4]$](graphics/JGJ3NW0T.png) car dérivable
car dérivable
De
plus elle est croissante sur
![$[2,3~;~2,4]$](graphics/JGJ3NW0V.png) et la calculatrice donne
et la calculatrice donne
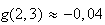 et
et
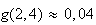 .
.
Donc
d'après le théorème des valeurs intermédiaires, il
existe
x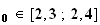
tel que
g(x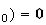
2)a) On a par définition :
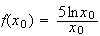
Or
g(x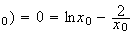
D'où
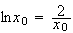
Donc
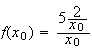
f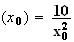 .
.
b)
Soit a un réel tel que
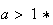
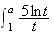 d
d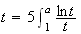 d
d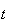
On fait une intégration par parties. On pose :
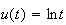
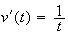
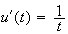
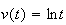
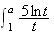 d
d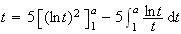 .
.
2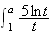 d
d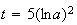
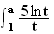 d
d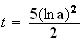
3)
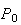 est le point d'intersection entre la courbe représentative de g et l'axe
des abcisses d'équation y=0.
est le point d'intersection entre la courbe représentative de g et l'axe
des abcisses d'équation y=0.
Donc
g(x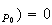
Donc
d'après la question 1,
x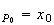
De
plus par sa définition,
M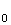 a pour coordonnées
(
a pour coordonnées
( 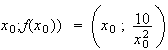 d'après 2a).
d'après 2a).
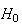 a pour coordonnées
:
a pour coordonnées
: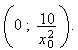
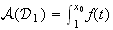 d
d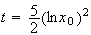 (d'après la question 2)b) avec
(d'après la question 2)b) avec
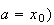
Or
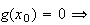
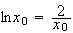
D'où
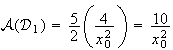
De
plus
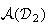 .représente
l'aire du rectangle de largueur 1 et de longueur
.représente
l'aire du rectangle de largueur 1 et de longueur
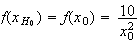
Donc
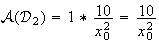
Donc
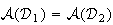
Les
domaines
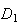 et
et
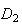 ont donc même aire.
ont donc même aire.
Cherchons maintenant un encadrement de cette aire.
D'après la question 1) on a :
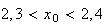
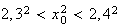 car la fonction x
car la fonction x
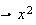 est croissante pour x
est croissante pour x
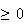
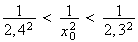
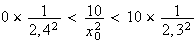
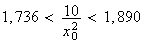
Finalement, on a donc :
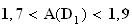 à
à
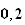 près.
près.

