CORRIGE de Mathématiques-Informatique
France Métropolitaine - Section S - Juin 2006
Exercice 1 :
1) Réponse : A
Pour savoir si le jeu est favorable au joueur, on calcule l'espérance de ce jeu.
Espérance du jeu :
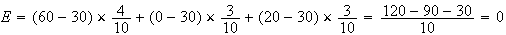
Le jeu est donc équitable.
2) Réponse : B
Pour trouver la probabilité de l'évènement "tirer au moins une fois un bulletin oui" , on calcule la probabilité que l'on note p de son évènement contraire "ne jamais tirer un oui".
La
probabilité qu'il ne tire pas de oui lors d'une partie est de
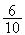
Les
parties étant indépendantes, la probabilité qu'il ne tire pas de
oui au bout de 4 parties est donc de
(
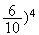donc
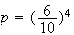
La probabilité cherchée est donc :
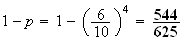
3) Réponse : C
Il
y a
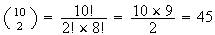tirages différents.
Les possibilités de tirages différents sont : oui-blanc, oui-non et non-blanc
Leur
nombre est égal à
.
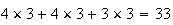La
probabilité qu'il obtienne un tirage de 2 bulletins de sortes
différents est donc :
.
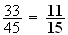