CORRIGE de Mathématiques-Informatique
France Métropolitaine - Section S - Juin 2006
Partie A :
1)a)
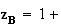 i
i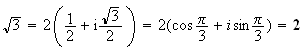 e
e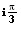
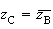 ,
donc
,
donc
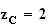 e
e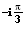
b) Faire la figure
2)
On a
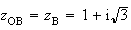
et
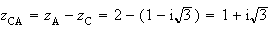
Donc
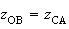
Donc
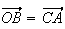
Le quadrilatère OBAC est donc un parallélogramme
De plus C est le conjugué de B donc OB=OC
Le quadrilatère OBAC est donc un losange.
3) Soit M un poit d'affixe z
On cherche l'ensemble des points M tels que :
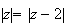
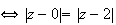
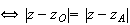
 O
O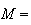 A
A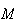
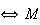 est donc équidistant de O et de A
est donc équidistant de O et de A
 donc
donc
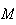 appartient à la médiatrice du segment [OA]
appartient à la médiatrice du segment [OA]
Or OBAC est un losange donc ses diagonales (OA) et (BC) sont perpendiculaires entre elles.
Donc l'ensemble des points M cherché est la droite (BC).
Partie B :
1)a)
Pour
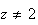 , on a :
, on a :
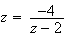
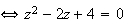
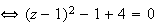
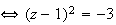
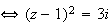
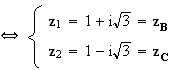
b)
D'après la question précédente, les solutions de
l'équation précédente sont les affixes des points B et C qui
sont donc les points invariants de l'application qui à
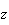
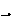
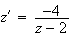 .
.
Donc
B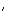 = B et
C
= B et
C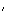 = C.
= C.
c)
 centre de gravité du triangle ABC.
centre de gravité du triangle ABC.
Donc
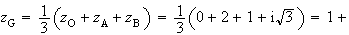 i
i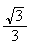
De plus par définition de G' on a :
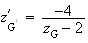
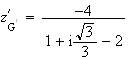
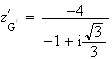
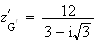
En multipliant par l'expression conjuguée du dénominateur, on obtient :
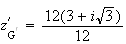
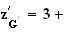 i
i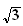
2)a) En utilisant le pré requis de l'énoncé, on peut écrire :
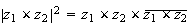
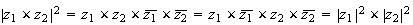
Donc
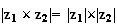
b)
Pour tout
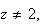 on a :
on a :
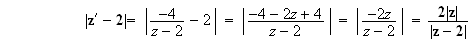 .
.
c)
Soit
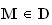
 O
a pour tout z :
O
a pour tout z :
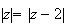
Or
d'après la question 2)b)
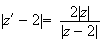
Donc
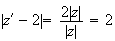
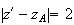
Donc
M' appartient au cercle
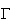 de centre A et de rayon 2.
de centre A et de rayon 2.

