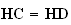CORRIGE MATHEMATIQUES Centres étrangers
SECTION S - JUIN
2005
1)
Pour montrer que la droite
(AA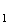 )
est orthogonale au plan (BCD), il suffit de montrer que
)
est orthogonale au plan (BCD), il suffit de montrer que
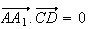 et
et
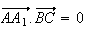
Calculons
tout d'abord
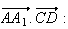
A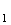 est centre de gravité du triangle BCD , donc :
est centre de gravité du triangle BCD , donc :
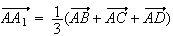
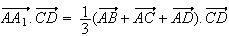
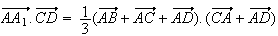
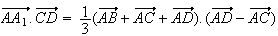
Or
les triangles ACD, ABC et ABD sont rectangles en A, donc
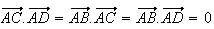
On en déduit en devellopant que :
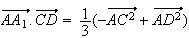
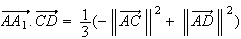
Or
ACD est un triangle isocèle de sommet A, donc
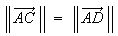
Donc :
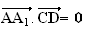
On
démontre de la même façon que
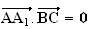 en décomposant
en décomposant
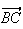 en
en
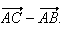
Conclusion
: La droite
(AA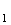 )
est donc orthogonale au plan (BCD).
)
est donc orthogonale au plan (BCD).
2) Première façon pour calculer l'aire du tétraèdre ABCD :
On
a vu que
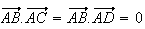
Donc la droite (AB) est orthogonale au plan (ACD).
Donc le volume du tétraède ABCD est égal à :
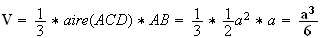
Deuxième façon pour calculer l'aire du tétraèdre ABCD :
On
a vu à la question 1 que la droite
(AA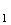 )
était orthogonale au plan (BCD).
)
était orthogonale au plan (BCD).
Donc
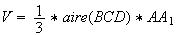
Or
le triangle BCD est équilatéral de coté
a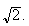 En
effet , c'est l'hypothénuse d'un triangle rectangle isocèle dont la
longueur du petit côté est a.( Pour le redémontrer, passer par
pythagore)
En
effet , c'est l'hypothénuse d'un triangle rectangle isocèle dont la
longueur du petit côté est a.( Pour le redémontrer, passer par
pythagore)
Donc l'aire de BCD s'écrit :
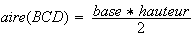
avec
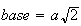
hauteur
=
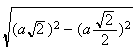 d'après pythagore
d'après pythagore
hauteur
=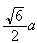
d'où
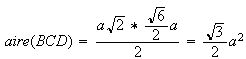
d'où
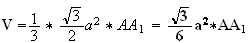
Calcul
de
AA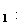
En égalant les deux expressions précédentes de V on déduit que :
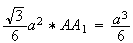
d'où
:
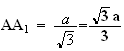
3)a) G est l'isobarycentre de ABCD, donc :
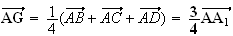 car
car
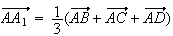
Donc
G appartient au segment
[AA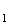 ]
]
De plus en passant à la norme dans l'expression précédente, on a :
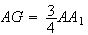
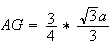 d'après la question 2.
d'après la question 2.
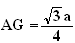
b) On cherche l'ensemble des points M tels que :
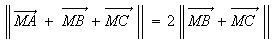
Or G est l'isobarycentre de ABCD donc :
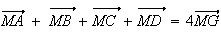
Or I milieu de [BC], donc :
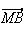 +
+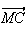 =2
=2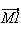
Cela revient donc à chercher les points M tels que :
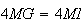 soit MG=MI
soit MG=MI
L'ensemble cherché est donc le plan médiateur du segment [GI].
4) a) G est l'isobarycentre de ABCD, donc :
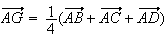
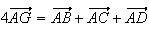
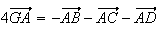
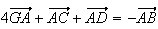
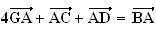
b)
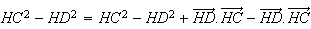
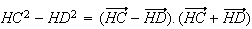
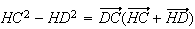
Or
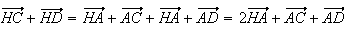
De
plus H est le symétrique de A par raaport à G donc
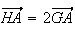
d'où
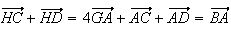
d'où
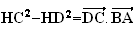
c) D'apres 3b)
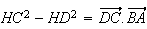
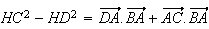
Or les triangles ABC et ABD sont rectangles en A, donc :
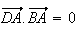 et
et
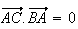
Donc :