CORRIGE MATHEMATIQUES Centres étrangers
SECTION S - JUIN
2005
1) Si M appartient à E on a :
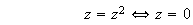 ou
ou
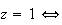 M=O ou M=B
M=O ou M=B
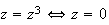 ou
ou
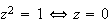 ou
ou
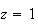 ou
ou
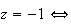 M=O ou M=Aou M=B
M=O ou M=Aou M=B
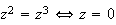 ou
ou
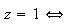 M=O ou M=B
M=O ou M=B
Donc
si M appartien à E, les nombres complexes z,
z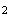 et
z
et
z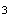 sont distincts .
sont distincts .
Donc les points M,N,P sont distincts 2 à 2.
2)a) D'après Pythagore, MNP est rectangle en P SSI :
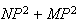 =MN
=MN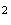
Or
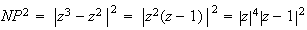
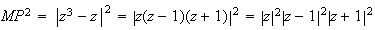
MN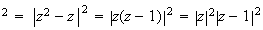
Donc
MNP est rectangle en P SSI
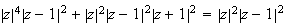
SSI
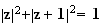 car
M
car
M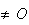 et
M
et
M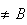 (
(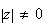 et
et
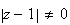 )
)
b)
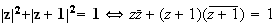
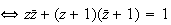
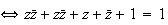
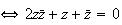
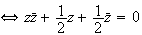
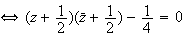
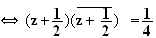
c) L'ensemble Cdes points M cherchés est tel que :
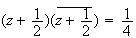
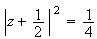
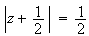
Soit
H le point d'affixe
-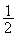
Ainsi
: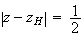
Cela
équivaut à
HM=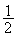
M
appartient donc au cercle de centre H et de rayon
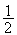 ,
qui est le cercle diamètre [OA].
,
qui est le cercle diamètre [OA].
Le point O et le point A appartiennent à ce cercle
Or
M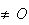 et
M
et
M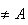
Donc l'ensemble des points M cherchés est le cercle de diamètre [OA] privé de O et A.
3)a)
Soit M d'affixe
z=re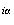
On
cherche l'ensemble des points M tels que l'affixe de P soit un réel
strictement positif.ie tel que
z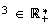
Or
z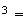 r
r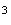 e
e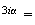 r
r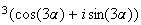
z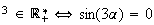 et
et
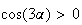 car r >0
car r >0
z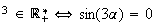 et
et
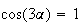
z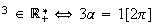
Or
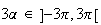
Donc
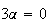 ou
-2
ou
-2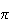 ou
2
ou
2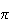
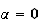 ou
-
ou
-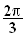 ou
ou
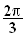
Rappel
: Dire que
z=re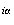 avec
r >0 signifie que M appartient à la demi droite ouverte d'origine O et
de vecteur directeur
(cos
avec
r >0 signifie que M appartient à la demi droite ouverte d'origine O et
de vecteur directeur
(cos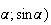 que l'on note
d
que l'on note
d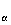
Donc l'ensemble des points M tel que l'affixe de P soit un réel strictement positif est la réunion de trois demi droites du plan d'origine O, et de vecteurs directeurs
respectifs
d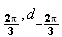 et
d
et
d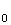
b) Représentation graphique (a faire soi même)
c) D'après les questions 2 et 3)a) , pour que le triangle MNP soit recatngle en P et que P soit un réel strictement positif, il faut et il suffit que :
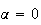 ou
-
ou
-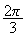 ou
ou
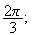 r >0 et que
r >0 et que
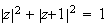
si
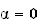 ;
;
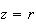 et
et
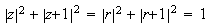 ce qui est impossible car r > 0. Il n'y a pas de
solutions.
ce qui est impossible car r > 0. Il n'y a pas de
solutions.
si
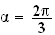 ;
z=re
;
z=re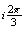 et
et
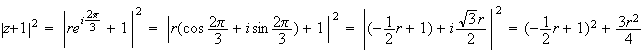
d'où
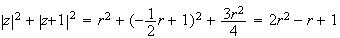
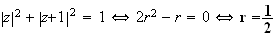
si
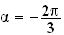 , on démontre de même que
, on démontre de même que
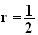
Les affixes des points M tel que le triangle MNP soit recatngle en P et que P soit un réel strictement positif sont :
z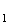 =
=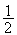 e
e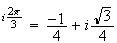
z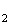 =
=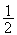 e
e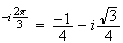
Les
points recherchés sont donc les 2 points d'affixe respectives
(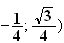 et
(
et
(