CORRIGE MATHEMATIQUES Centres étrangers
SECTION S - JUIN
2005
1)
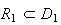
Donc
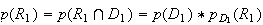
Or
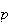 (
(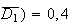 et donc
et donc
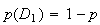 (
(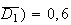
et
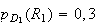
Donc
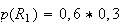
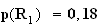
2)
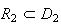
Donc
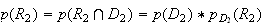
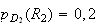
Calcul
de
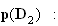
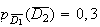 car pour que la personne ne décroche pas la seconde fois, il faut qu'elle
n'est pas décroché la première fois et ait été
rappelé .
car pour que la personne ne décroche pas la seconde fois, il faut qu'elle
n'est pas décroché la première fois et ait été
rappelé .
et
donc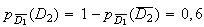
Comme
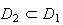
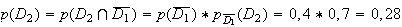
Retour
sur calcul de
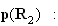
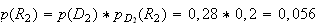
Calcul de p(R) :
R
est la réunion disjointe de
R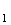 et
R
et
R Donc
Donc
p(R)=p(R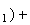 p(R
p(R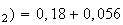
p(R)=0,236
3)
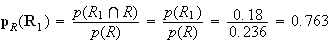 à
10
à
10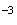 près
près
4) D'après la question 2, la probalité pour que la personne réponde au questionnaire est p(R)=0,236
Soit X le nombre de personnes qui répondent au questionnaire.
X est une variable aléatoire qui suit une loi binomiale de paramètre (25, p(R))
La
probalité pour que 20% des personnes repondent aux questionnaires
est donc la probalité telle que
P(X=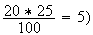
P(X
= 5)
=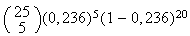
P(X
= 5) =0,179 à
10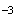 près.
près.

