CORRIGE MATHEMATIQUES Amérique du Nord
SECTION S - JUIN
2005
Exercice 4 :
1)a)
Si le dé indique 1, on tire une boule dans une urne contenant 4 voyelles et 6 consonnes et on gagne si on tire une voyelle. On obtient :
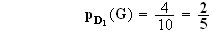
Si le dé indique 2, on tire deux boules simultanément et on gagne si on tire 2 voyelles. On obtient :
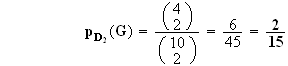
Si le dé indique 3, on tire trois boules simultanément et on gagne si on tire 3 voyelles. On obtient :
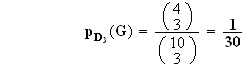
b)
D'après la formule des probabilités totales on a :
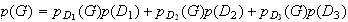
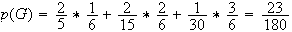
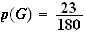
2)
Il s'agit de calculer la probabilités que le joueur a de tomber sur le 1 sachant qu'il a gagné.
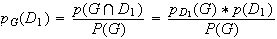
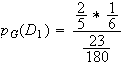
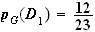
3)
Soit X : le nombre de partie gagnée.
On
a vu à la question 1, que la probabilités de gagner une partie
était de
.
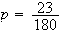Le joueur joue six fois .Ces épreuves sont indépendantes.
Le nombre X suit une loi binomiale de paramètre (6;p)
Donc la probabilités que le joueur gagne exactement 2 parties est p(X=2).
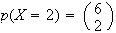
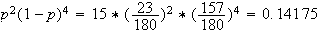
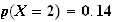à
10
prés
Nombre minimal de parties n pour que la probabilités d'en gagner une soit supérieure à 0,9 :
La probabilités de gagner au moins une partie est :
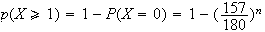
On
veut que
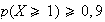
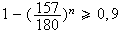
Soit
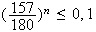
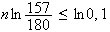la fonction logarithme étant croissante
Or
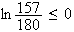
Donc
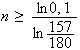(le sens de l'inégalité change)
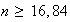
n étant un entier, il faut donc 17 parties minimum pour que la probabilités d'en gagner une soit supérieure à 0,9.
