CORRIGE MATHEMATIQUES Amérique du Nord
SECTION S - JUIN
2005
Exercice 2 :
1.
Pour tout x
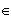
![$\left[ 0;2\right] $](graphics/J9EOJRL3.png) ,
on a :
,
on a :
f(x)
=
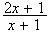
f'(x)
=
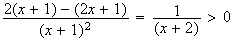
Donc f est strictement croissante sur [0,2].
On
peut en déduire que si x
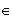
![$\left[ 1;2\right] $](graphics/J9EOJRLB.png) alors f(x)
alors f(x)
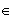
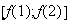
Ici
f(1) =
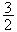 > 1 et f(2)
=
> 1 et f(2)
=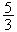 < 2
< 2
Donc
f(x)
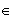
![$\left[ 1;2\right] $](graphics/J9EOJRLN.png)
2.a)
D'après le graphique(faire le dessin), il semble que la suite
u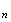 soit
croissante et la suite
v
soit
croissante et la suite
v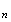 soit
décroissante
soit
décroissante
et qu'elles soient toutes les deux convergentes vers la même limite.
b)
Montrons, par récurrence, que pour tout entier naturel n, 1
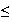 v
v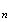
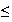 2
2
Pour n=0 :
v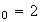 donc 1
donc 1
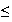 v
v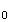
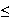 2
2
n
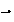 n+1
n+1
Supposons
que 1
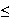 v
v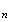
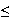 2 alors d'après la question 1, 1
2 alors d'après la question 1, 1
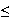 f(v
f(v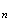 )
)
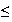 2
2
Or
f(v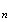 )
=
v
)
=
v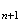
Donc
1
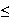 v
v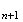
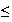 2
2
Donc
pour tout entier naturel n, 1
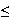 v
v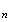
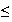 2
2
Démontrons
maintenant par récurrence que, pour tout entier naturel n, on a
v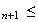 v
v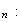
Pour n=0 :
v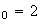 et
v
et
v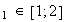 donc
v
donc
v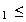 v
v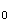
n
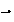 n+1
n+1
Supposons
que
v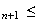 v
v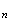 ,
il faut alors montrer que
v
,
il faut alors montrer que
v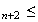 v
v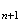
f
étant croissante sur [1;2], on a
f(v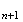 )
)
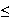 f(v
f(v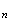 )
)
Donc
v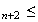 v
v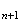
Conclusion
: Pour tout entier naturel n, on a
v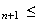 v
v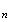
c)
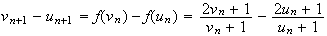
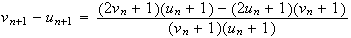
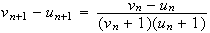
Montrons
maintenant par récurrence que pour tout entier naturel n,
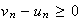
Pour n=0
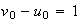
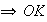
n
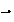 n+1
n+1
Supposons
que
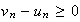 ,
alors d'après le calcul précédent,
,
alors d'après le calcul précédent,
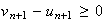 car
car
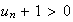 et
et
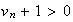
Conclusion
: Pour tout entier naturel n,
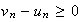
De
plus
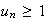 et
et
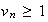 ,
donc
,
donc
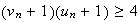
Donc
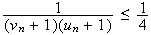
En
multipliant de chaque coté de l'inégalité par
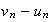 qui est positif on obtient :
qui est positif on obtient :
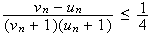
Donc:
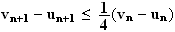
d)
Montrons maintenant par récurrence sur n que pour tout entier naturel
n, on a
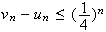
Pour n=0 :
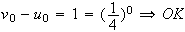 verifié
verifié
n
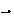 n+1
n+1
Supposons
que
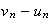
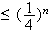
On a alors d'aprés 2)d :
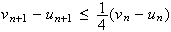
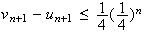 d'après l'hypothèse de récurrence
d'après l'hypothèse de récurrence
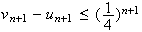
Donc :
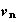
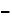
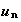
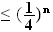
e)
La suite
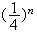 est une suite géométrique de raison
est une suite géométrique de raison
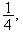 donc comme toute suite géométrique , elle converge vers 0.
donc comme toute suite géométrique , elle converge vers 0.
Or
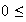
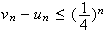
En passant à la limite à gauche et à droite de l'inégalité , par encadrement on obtient :
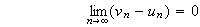
Les
suites
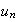 et
et
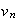 vérifient les propriétés suivantes :
vérifient les propriétés suivantes :
-
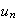 est croissante
est croissante
- 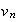 est décroissante
est décroissante
-
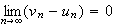
 Les
suites
Les
suites
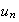 et
et
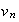 sont
adjacentes. Ainsi, elles convergent vers la même limite, que l'on note
sont
adjacentes. Ainsi, elles convergent vers la même limite, que l'on note
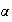
Déterminons
maintenant la valeur de
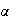 :
:
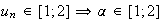
On
a pour tout entier naturel,
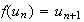 (*)
(*)
Or
f est continue sur
![$[1;2]$](graphics/J9EOJRQR.png) ,
donc
,
donc
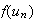 converge vers
converge vers
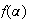
De
plus
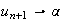 car
car
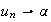
Donc en passant à la limite dans l'égalité (*), par unicité de la limite on a :
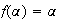
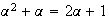
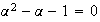
Résolution
de cette équation du second degré en
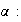
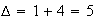
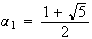
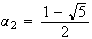
Or
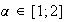
Donc