Exercice 1 :
1. Pour savoir si le triangle ABC est isocèle, calculons les distances AB, BC et CD :
AB
=
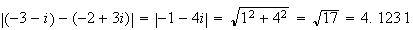
AC
=
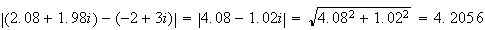
BC
=
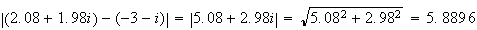
On
remarque que AB
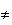BC
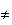CD, donc le triangle ABC n'est pas isocèle.
Pour
savoir maintenant si le triangle est rectangle en A, calculons l'angle
(
;
)
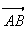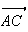On
a
(
;
)
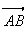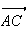= arg
=
arg
=
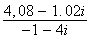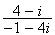arg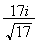
= arg i =
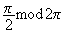
Donc le triangle ABC est bien rectangle en A.
La réponse exacte est donc la réponse b.
2.
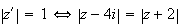
Si on note G et H les points d'affixe respectives 4i et -2 , on a alors :
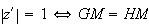
Donc
l'ensemble des ponts M tels que
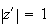est la médiatrice de [EF].
C'est donc une droite. La réponse exacte est donc la réponse b.
3.
On peut écrire
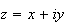pour tout
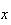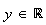et
et
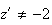
Alors z' devient :
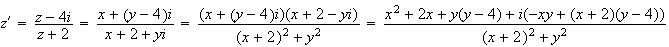
z'
est réel
La partie imaginaire de z' est nulle
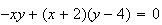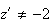
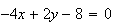et
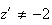
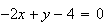et
et
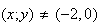
L'ensemble
des points M tel que z' est réel est donc une droite
d'équation
y
= 2x +4 privée d'un point de coordonnée (-2;0).
La réponse exacte est donc la réponse b.
4.
L'ecriture complexe de la rotation de centre D et d'angle
-
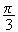est :
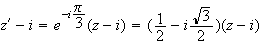
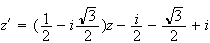
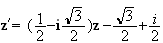
La réponse exacte est donc la réponse a
