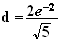CORRIGE MATHEMATIQUES Amérique du Nord
SECTION S - JUIN
2005
Exercice 3 :
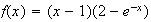
1.a)
Limite de f en +
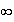 :
:
On
a
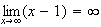 et
et
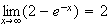
Donc :
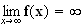
b)
Pour que la droite d'équation y = 2x - 2 soit asymptote à
C, il faut montrer que la limite de (f(x) - (2x - 2))
,quand x tend vers
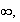
tend vers 0.
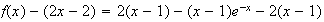
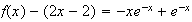
Or
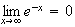
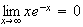 car l'exponentielle l'emporte sur la puissance
car l'exponentielle l'emporte sur la puissance
On en déduit que :
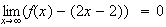
Donc la droite d'équation y = 2x - 2 est asymptote à C.
c)
position relative de C par rapport à
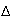 :
:
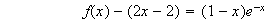
Or
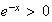
Donc
le signe de
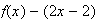 dépend du signe de
dépend du signe de
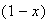
-
Sur [0,1],
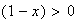 ,donc
,donc
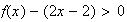 ,
donc la courbe C est au dessus de son asymptote
,
donc la courbe C est au dessus de son asymptote
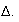
-
Sur
[1,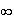 ],
],
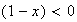 ,donc
,donc
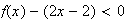 ,
donc la courbe C est en dessous de son asymptote
,
donc la courbe C est en dessous de son asymptote
2-a)
Pour tout réel x on a :
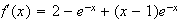
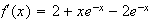
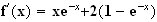
b)
Pour
tout x >0 ,
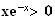
De
plus
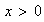
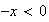
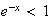 car la fonction exponentielle est une fonction croissante sur
car la fonction exponentielle est une fonction croissante sur
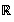


Donc
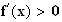
c)
On trouve : f'(0)=0
Tableau de variation de f :
____________________________________________
x0+
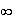
____________________________________________
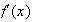 0+
0+
____________________________________________
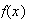 -1
-1 +
+
3)
On
cherche l'aire du domaine plan limité par C, la
droite
 et les droites d'équation x=1 et x=3
et les droites d'équation x=1 et x=3
Or
, on a démontré à la question 1 , que C était au dessous
de
 pour x >1. L'aire cherchée est donc égale à :
pour x >1. L'aire cherchée est donc égale à :
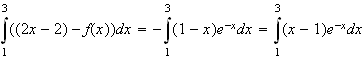
On fait une intégration par partie :
On pose :
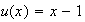
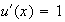
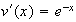
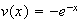
d'où :
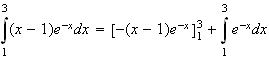
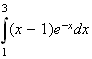
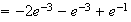
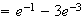
L'unité
d'aire étant de
4cm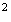 , l'aire
cherchée vaut :
, l'aire
cherchée vaut :
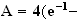
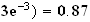
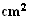
4)a)
Le
coefficient directeur de la droite
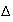 est 2
est 2
La
tangente à C au point d'abscisse x a pour
coefficient directeur : f'(x)=2 +
(x-2)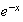
La
tangente à C est parallèle à
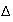 SSI le coefficient directeur de la droite
SSI le coefficient directeur de la droite
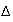 et le coefficient directeur de la tangente à C
sont égaux.
et le coefficient directeur de la tangente à C
sont égaux.
SSI f'(x)=2
SSI
(x-2)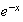 =0
=0
SSI x=2
Le
point A a donc pour coordonnées (2 ; 2 -
e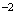 )
)
b)
Distance du point à la droite
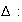
D'après
le cours, la distance d'un point
M(x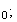 y
y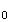 )
à la droite
)
à la droite
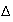 d'équation y=ax+by+c=0 s'écrit :
d'équation y=ax+by+c=0 s'écrit :
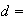
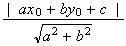
On
applique ici cette formule avec M=A=(2 ; 2 -
e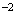 )
et y =2x-2 donc a=2 b=-1 et c= -2
)
et y =2x-2 donc a=2 b=-1 et c= -2
d'ou
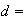
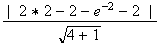
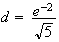
L'unité
de longueur étant de 2 cm, on trouve