CORRIGE MATHEMATIQUES FRANCE METROPOLITAINE
SECTION S - Septembre 2004
Exercice 4 :
1.Solution
de l'équation
:
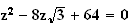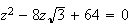
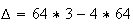
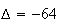
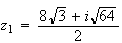
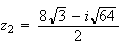
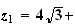
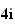
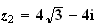
2.a)
,
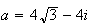donc
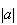
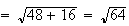= 8. On peut donc écrire :
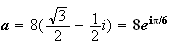
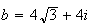est le conjuguée de a donc :
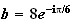
b) distance OA :
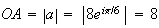
distance OB :
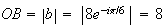
distance AB :
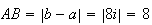
On constate que OA=OB=AB , donc le triangle OAB est un triangle équilatéral.
3.
D est l'image de C par la rotation de centre O et d'angle
-
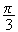.Donc l'affixe de D s'écrit :
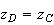
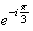
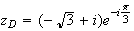
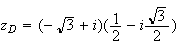
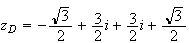
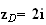
4.a) Le point G existe car la somme des coefficients est égale à 1, donc non nulle.
Par définition du barycentre, on a :
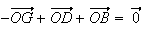
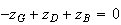
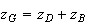
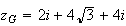
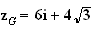
b) voir graphique
c)
Calculons tout d'abord l'affixe du vecteur
:
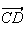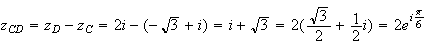
Calculons
maintenant l'affixe du vecteur
:
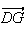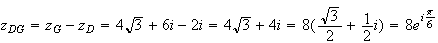
Les
vecteurs
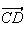et
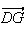ont
donc le même argument.
Les points C, D,G sont donc alignés.
d) Par définition du barycentre, on a :
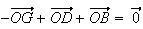
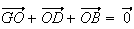
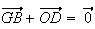(d'après Chasles)
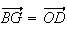
BGDO est donc un parallélogramme.
4. Calculons la distance GA :
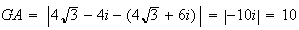
De même la distance CA s'écrit :
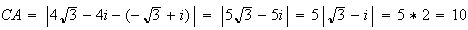
Enfin la distance CG s'écrit :
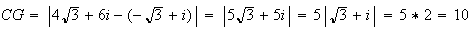
On constate donc que GA=CA=CG.
Donc le triangle AGC est équilatéral.
