CORRIGE MATHEMATIQUES FRANCE METROPOLITAINE
SECTION S - Septembre 2004
Exercice 2 :
1. x > 0 et y >0
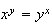
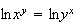
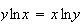
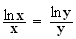
2.a)
Limite de h en +
On
sait que
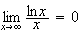donc
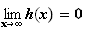
Limite de h en 0 :
On
sait que
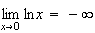et
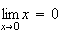
donc
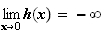car x est strictement positif.
b) Calcul de la dérivée de h :
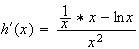
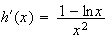
Le
signe de h'(x) dépend donc du signe de
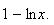
Or
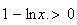lorsque
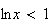c'est à dire
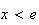
et
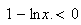lorsque
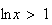c'est à dire
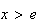
d'ou le tableau de variation :
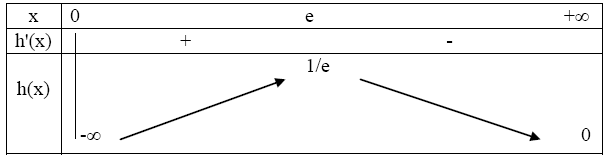
On
a vu que la dérivée de h s'annulait pour x=e. Donc le maximum de h
est atteint pour x =
x
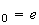et
h(x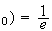
c) Intersection de la courbe C avec l'axe des abcisses :
L'intersection de la courbe C avec l'axe des abcisses est le point d'ordonnée nulle soit h(x)=0 soit x=1
3.
La fonction h est continue (car dérivable) strictement
croissante sur
![$\left] 1;e\right[ $](graphics/J9GOX55D.png)
,
h(1)=0 et
h(e)=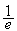
,
donc pour tout nombre
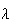élément de l'intervalle
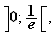il existe un et un seul nombre a
de
l'intervalle
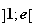tel que
h(a)=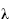
La
fonction h est continue (car dérivable) strictement décroissante sur
,
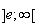h(e)=
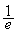et
,
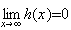donc pour tout nombre
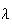élément de l'intervalle
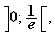il existe un et un seul
nombre
b de l'intervalle
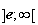tel que
h(b)=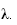
4.a)
Graphiquement, on lit :
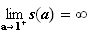
b)
Graphiquement, on lit :
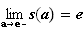
c) Tableau de variation de s :
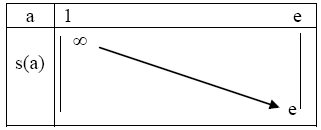
La
fonction s est décroissante sur
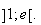
5)
Le seul entier possible pour a sur
![$\left] 1;e\right[ $](graphics/J9GOX569.png)
est le nombre 2 est on sait que
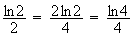donc b=4. Le seul couple d'entiers distincts solution de (E) est donc
le couple (2 ; 4)
