CORRIGE MATHEMATIQUES FRANCE METROPOLITAINE
SECTION S - Septembre 2004
Exercice 3 :
Partie A :
1.
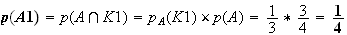
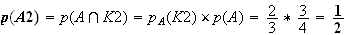
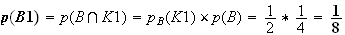
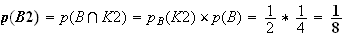
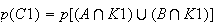
les événements A1 et B1 sont incompatibles)
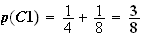
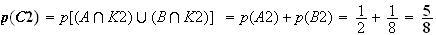
2. L'expérience décrite suit une loi de Bernoulli de paramètre n=5
D'où
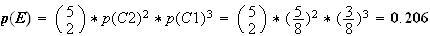
La probalité d'obtenir deux particules dans K2 quand on en a projeté 5 est donc de 0.206
Partie B :
1. La demi vie des particules de type A est de 5730 donc pour t =5730, on a :
=
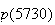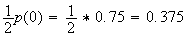
De
plus
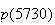=0.75e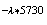
d'où
:
0.75e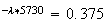
e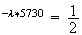
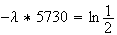
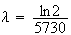
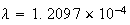
Une
valeur approchée à
10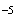
près
de
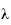est
0,00012
2.On cherche le temps t au bout duquel 10% des particules A sont transformés en particules de types B . Au bout de t années, il restera 90% de la quantité initiale .
Donc t vérifie l'équation suivante :
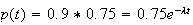
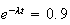
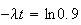
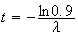
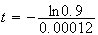
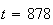
Les particules A sont donc transformés en particules de types B au bout de 878 années.
3. Il y aura autant de particules A que de particules B lorsque :
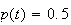
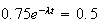
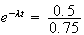
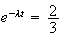
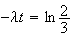
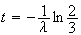
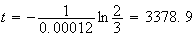
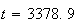
Une valeur approchée arrondie à l'unité est 3379.
Il y aura donc autant de particules de type A que de type B au bout de 3379 ans.
