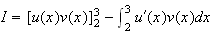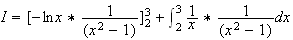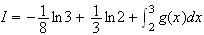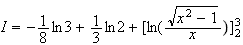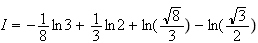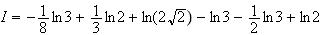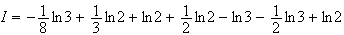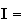CORRIGE MATHEMATIQUES FRANCE METROPOLITAINE
SECTION S - Septembre 2004
Exercice 1 :
1.a)
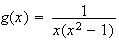
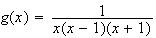
On cherche a,b,c tels que :
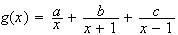
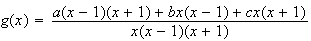
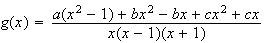
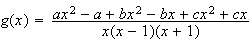
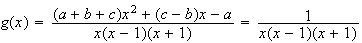
Par identification , on obtient le système suivant :
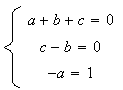
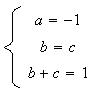
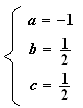
b) D'après a) on a :
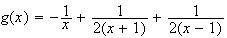
Donc une primitive G de g sur ]1 ; +∞[ est :
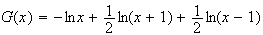
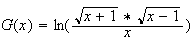
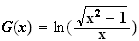
2.
Posons
,
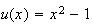alors
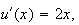donc
une primitive de
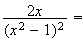
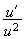est :
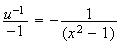
Donc une primitive F de f sur l\intervalle ]1 ; +\[.est :
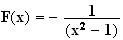
3.Calcul de I :
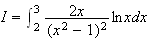
On fait une intégration par partie. On pose :
=
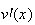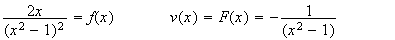(d'après
2)
