Partie A :
1.a) D'après l'arbre pondéré des événements, la probabilités de U sachant D est :
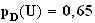
b)
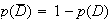
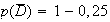
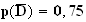
2.a) La probabilités que le DVD choisi ait été reçu par dotation et soit de production européenne est :
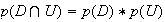
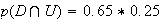
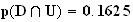
b)
On cherche la probabilités que le DVD ait été acheté et soit
de production européenne ce qui revient à chercher
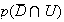
Or
les évènements D et
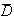sont incompatibles donc U = (U∩D) U
(U∩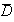
)
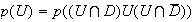
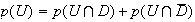(d'après la formule des probabilités totales)
d'ou :
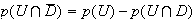
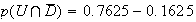
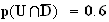
3. La probabilités telle que le DVD soit de production Européenne sachant qu'il a été acheté est :
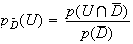
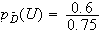
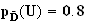
Partie B :
Soit X l'événement le DVD a été reçu en dotation .
La loi de probabilités associé à l'expérience est une loi binomiale de paramètre de paramètre 3 (car 3 tirages successifs) et 0,25 (probabilités que le DVD soit reçu en dotation):
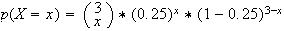
Ainsi la probabilités de l'événement " exactement deux des trois DVD choisis ont été reçus en dotation " revient à chercher p(X=2)
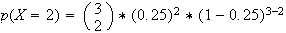
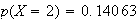
Arrondie au millième, la probabilités de l'événement " exactement deux des trois DVD choisis ont été reçus en dotation " est 0,141
