a)
L'équation f(x)=4 admet exactement 2 solutions dans l'intervalle [-3 ; +
]
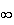: FAUX
Justification
: On trace la droite y= 4 sur le graphique et on constate que cette droite
coupe 3 fois la courbe
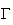représentative de f.
L'équation
f(x)=4 admet donc exactement 3 solutions dans l'intervalle [-3 ; +
].
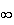b)
:
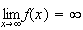VRAI
Justification : voir graphique
c)
:
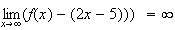FAUX
Justification
: La droite y=2x-5 est asymptote à
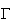en
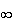. Donc
d'aprés la définition d'une asymptote :
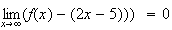
d) f'(0)=1 : FAUX
Justification
: Le coefficient directeur de la tangente à la courbe
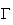au point d'abscisse 0 est négatif , donc f'(0) < 0
e) f'(x) >0 pour tout réel x appartenant à [-2,1] : FAUX
Justification : La fonction f n'est pas monotone sur l'intervalle [-2,1]. En effet on peut voir sur le graphique que f est croissante sur [-2,-1] puis décroissante sur [-1,1]
f)
:
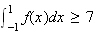VRAI
Justification
: La fonction f sur [-1,1] est strictement positive. Donc
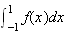représente l'aire du domaine D limité par la courbe
,
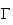l'axe des abscisses, la droite d'équation x=1 et l
la droite d'équation x=-1
Or on constate sur le graphique que l'aire du domaine D est supérieur à 7 (en unité d'aire ).
