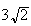Exercice 3 :
1)a)Un
vecteur normal au plan
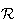est le vecteur
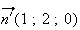
Pour
montrer que les plans
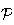et
sont perpendiculaires, il suffit de montrer que leurs vecteurs normaux
respectifs sont orthogonaux entre eux.
Or
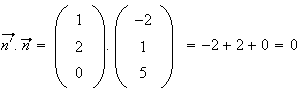
Donc
les vecteurs
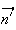et
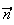sont orthogonaux.
Donc
les plans
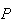et
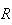sont
perpendiculaires.
b)
Commençons par déterminer une équation du plan
.
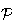Soit
M de coordonnée (x ; y ; z) avec x, y, z
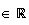
M
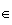
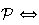
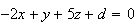avec d
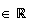(car un vecteur normal au plan
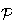est le vecteur
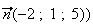
De
plus B
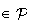
Donc :
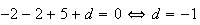
Donc
une équation de
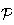est :
.
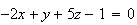Les points communs aux deux plans vérifient les deux équations de plans .
Ainsi on a
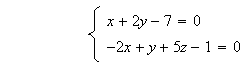
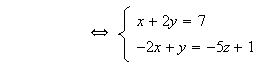
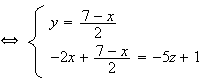
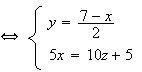
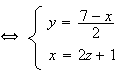
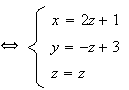
Les
deux plans étant perpendiculaires, leur intersection est bien une droite
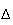défini par les équations
:
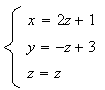
Si on remplace z par t on obtient l'équation paramétrique de cette droite.:
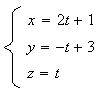
On
peut donc en déduire que cette droite a pour coefficient
directeur
(
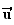2 ; -1 ; 1)
De
plus pour
,
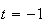les équations deviennent :
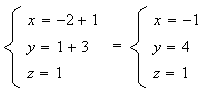
Donc
le point C appartient à la droite
c)
distance du point A au plan
:
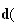A
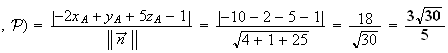
distance
du point A au plan
:
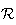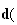A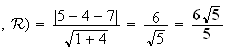
d)
Pour trouver la distance du point A à la droite
,
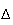on applique le théorème de Pythagore dans le plan contenant A et
perpendiculaire aux deux plans
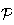et
:
.
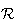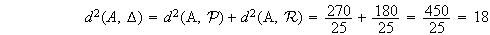D'où :
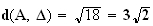
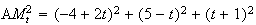
2)a)
A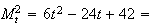
.
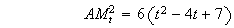Le
trinôme
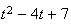a pour discriminant
.
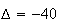Il ne s'annule donc pas et est positif pour tout réel t (car le
coefficient de
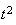positif)
.
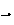
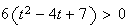
Donc
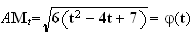
b)
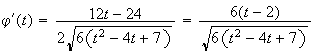
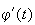est du signe de
(
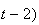car
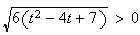
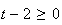
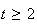
Donc
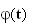est
décroissante sur [0 ; 2], puis croissante sur
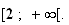
Elle
admet un minimum en
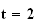qui
vaut
.
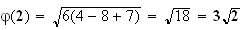c)
D'après la question 1. b.,
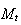est un point de la droite
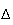
De
plus on a vu à la question 1. d. que la plus courte
distance de A à
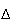était égale à
.
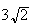On
aurait donc pu prévoir sans calcul que le minimum de
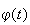était
