Exercice 1 :
Partie A :
1)
limite de f en
+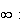
On
pose
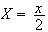
f(x) devient :
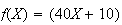 e
e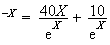
Or
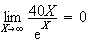 par croissance comparé
par croissance comparé
et
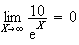
Donc
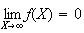
Or
lorsque
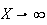 ,
,
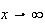
Donc
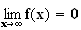
2) Pour étudier les variations de f, on calcule sa dérivée :
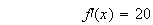 e
e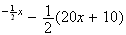 e
e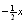
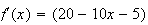 e
e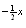
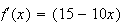 e
e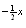
e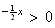 pour tout x >0
pour tout x >0
Le
signe de la dérivée dépend donc uniquement du signe de
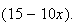
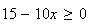
x
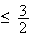
D'où le tableau de variation de f :
____________________________________________
x 0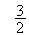 +
+
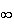
____________________________________________

____________________________________________
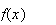 10
10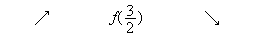 0
0
avec
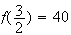 e
e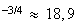
3)
Sur
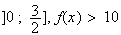 ,
donc l'équation
,
donc l'équation
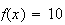 n'a pas de solution.
n'a pas de solution.
Sur
l'intervalle
![$]\dfrac{3}{2};$](graphics/HVRIXQBM.png)
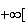 ,
la fonction
,
la fonction
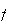 est continue (car dérivable), monotone décroissante de
est continue (car dérivable), monotone décroissante de
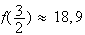 à
à
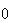 .
.
Il
existe donc un réel unique
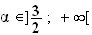 tel
que
tel
que
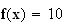 .
.
Grace
à la calculatrice, on trouve le résulat suivant
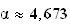 .
.
4) Courbe C :
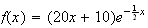
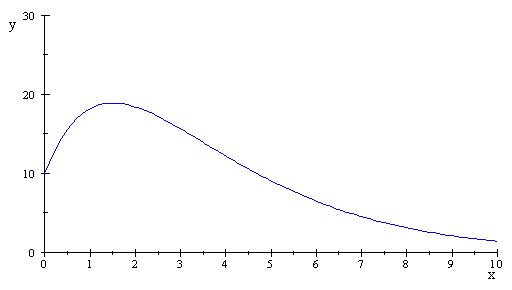
5)
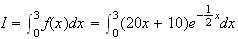
On fait une intégration par partie :
On pose :
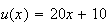 ;
;
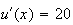
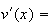 e
e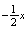 ;
;
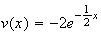
d'où :
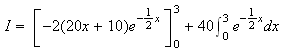
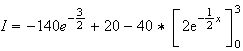
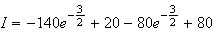
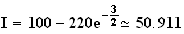
Partie B :
1)
f est solution de (E)
SSI 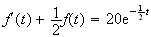 et
et
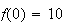
On
a bien
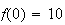
De plus :
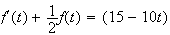 e
e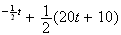 e
e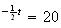 e
e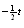
f
est donc solution de (E) sur
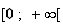 .
.
2)a)
Par définition on a pour tout
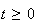 :
:
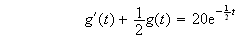 et
et
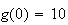 .
.
De
plus d'après la question précédente
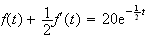
D'où par différence de ces deux équations :
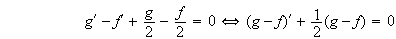 .
.
La
fonction
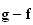 est
donc solution, sur l'intervalle
est
donc solution, sur l'intervalle
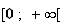 ,
de l'équation différentielle :
(E
,
de l'équation différentielle :
(E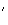 )
)
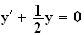 .
.
b)
(E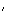 )
:
)
:
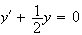
Les
solutions de l'équation
(E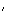 )
sont les fonctions
)
sont les fonctions
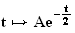 avec A
avec A
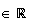
c)
La fonction
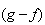 est une solution de (E') (d'après la question 2a))
est une solution de (E') (d'après la question 2a))
Donc
pour tout
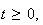 on a :
on a :
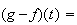 Ae
Ae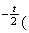 d'après
2b))
d'après
2b))
Or
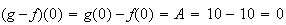 .
.
Donc
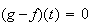
Donc
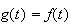
Conclusion
: l'équation différentielle (E) a une solution unique vérifiant
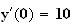 ,
c'est la fonction
,
c'est la fonction
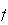 de
la partie A.
de
la partie A.
3)
D'après la question 3. de la partie A,
la température de la réaction chimique redescent à sa
valeur initiale ie
10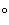 lorsque
lorsque
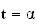
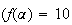 .),
.),
soit
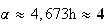 h
h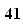 min
min
4)
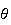 correspond à la valeur moyenne de f sur [0 ;
3
correspond à la valeur moyenne de f sur [0 ;
3![$]$](graphics/HVRIXRES.png) donc :
donc :
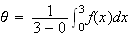
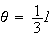
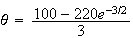 d'après la question 5 partie A.
d'après la question 5 partie A.
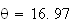 soit
17
soit
17 si
on arrondie au degré.
si
on arrondie au degré.

