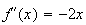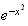Exercice 2 :
1) Réponse : C
Justification :
z
est le nombre complexe de module
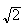 et d'argument
et d'argument
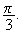 Donc
z s'écrit :
Donc
z s'écrit :
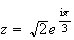
donc
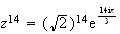
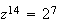 e
e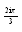
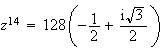
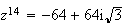 .
.
2) Réponse : D
Justification :
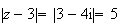
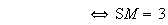
 appartient au cercle de centre S et de rayon 3.
appartient au cercle de centre S et de rayon 3.
3) Réponse : B
Justification :
D'après le théorème d'Al-Kashi la diagonale AC a pour longueur :
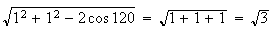 .
.
Or ACF est un triangle rectangle en A,
donc
.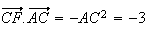
Or
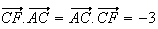
4) Réponse : A
Justification :
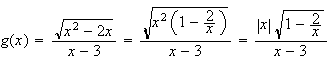
 Or
Or
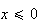 donc
donc
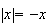
 D'où
:
D'où
:
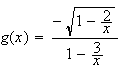
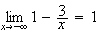
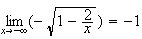
Donc
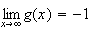
Donc
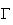 admet une asymptote d'équation
admet une asymptote d'équation
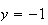 au voisinage de
-
au voisinage de
-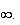
5) Réponse : C
Justification :
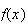 est par définition une primitive de la fonction
est par définition une primitive de la fonction
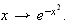
Donc
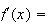
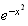
D'où