1) méthode plus rapide que celle proposée dans l'énoncé :
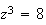
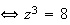 e
e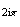
Si
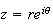 avec r
avec r
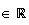 et
et
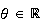
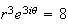 e
e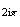
Egalité du module :
r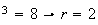
Egalité de l'argument :
3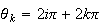 avec
avec
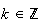
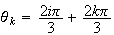
Il
y a donc trois solutions pour
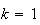 ,
,
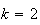 et
et
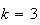 car
car
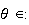
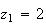 e
e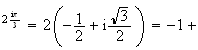 i
i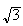
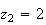 e
e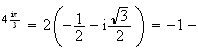 i
i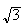
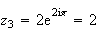 .
.
Donc
les solutions de l'équation
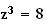 sont
:
sont
:
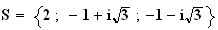
2)a) Figure
b)
B' est l'image de B par la rotation de centre A et d'angle
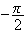 ,
donc :
,
donc :
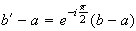
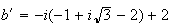
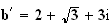 .
.
c)
C' est l'image de C par la rotation de centre A et d'angle
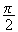 ,
donc :
,
donc :
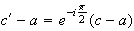
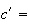 i
i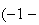 i
i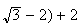
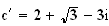 .
.
Donc
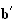 et
et
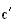 sont
bien conjuguées.
sont
bien conjuguées.
3)a)
N est le milieu de [BB'] donc
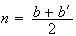
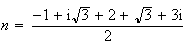
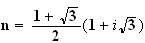 .
.
Alignement de O, N, C :
On
constate que
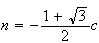
Les
vecteurs
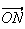 et
et
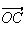 sont donc colinéaires.
sont donc colinéaires.
Donc les points O, N et C sont alignés.
b)
Q est le milieu de [BB'], N est le milieu de
[CC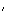 ]
]
Or
géométriquement,les segments
[BB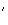 ]
et
[CC
]
et
[CC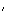 ]
sont symétriques autour de
(O
]
sont symétriques autour de
(O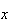 ).
).
Donc leurs milieux respectifs Q et N le sont aussi.
donc
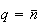
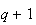
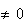 ,
calculons
,
calculons
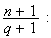
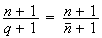
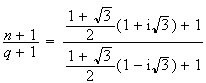
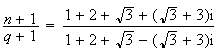
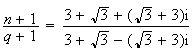
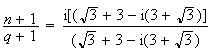
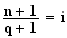
Etude du triangle MNQ :
M
étant le milieu de
![$\left[ CB\right] $](graphics/HVRGO94N.png)
on
a
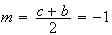
Or
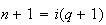
On remplace -1 par m dans l'équation précédente et on obtient :
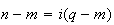
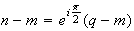
Donc
N est l'image de Q dans la rotation de centre M et d'angle
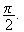
Le triangle MNQ est donc un triangle rectangle isocèle.
c)
P étant le milieu de
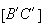
on
a
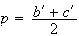
Or
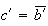 car C' est symétrique de B' par rapport à O.
car C' est symétrique de B' par rapport à O.
Donc
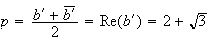
L'affixe
du milieu de
![$\left[ MP\right] $](graphics/HVRGO957.png) est
est
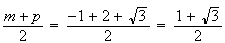
L'affixe
du milieu de
![$\left[ NQ\right] $](graphics/HVRGO95B.png) est
est
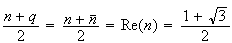
![$\left[ MP\right] $](graphics/HVRGO95F.png) et
et
![$\left[ NQ\right] $](graphics/HVRGO95H.png) ont donc le même milieu. MNPQ est donc un parallélogramme.
ont donc le même milieu. MNPQ est donc un parallélogramme.
De
plus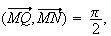 donc
MNPQ est un rectangle
donc
MNPQ est un rectangle
Enfin on MQ=MN, MNPQ est donc un rectangle à deux côtés consécutifs égaux.
C'est un carré
Le quadrilatère MNPQ est donc un carré.

