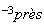1) On cherche la probalité telle que la montre tirée ne présente aucun des défauts c'est à dire la montre tirée ne présente ni le défaut a , ni le défaut b.
Donc
C l'évènement associé à cette probalité peut
s'écrire :
C=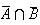
Donc
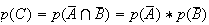car les évènements
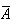et
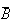sont indépendants.
Or
=
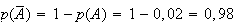
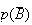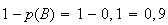
Donc
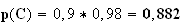
2)
Pour calculer la probalité de l'évènement D, on
calcule la probalité de son évènement contraire
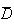"La montre présente les 2 défauts ou la montre ne présente
aucun défaut".
Donc
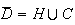
avec H l'évènement "La montre présente les 2 défauts ".
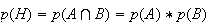car les évènements sont indépendants.
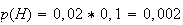
D'où
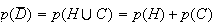car H et C sont des èvènements disjoints.
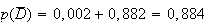
d'où :
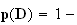
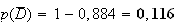
3)
X suit une loi binomiale de paramètres
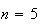et
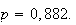
E est l'èvenement "4 montres au moins n'ont aucun défaut"
Donc
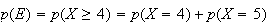
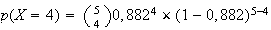
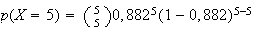
Finalement :
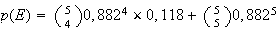
soit
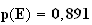à
10
