Partie A :
1)
a) Limite de f en +
:
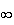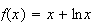
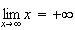
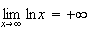
Donc
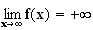
Limite de f en 0 :
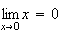
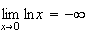
Donc
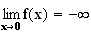
b)
.
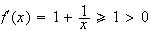car
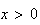
La
fonction est donc strictement croissante sur
.
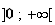2)a)
La fonction
est continue et croissante sur
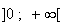
De
plus
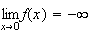et
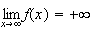
Donc
est une bijection de
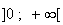sur
,
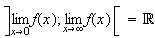Par
conséquent pour tout entier naturel
,
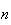il existe un unique antécédent
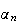
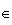
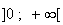tel
que
.
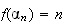b) Figure :
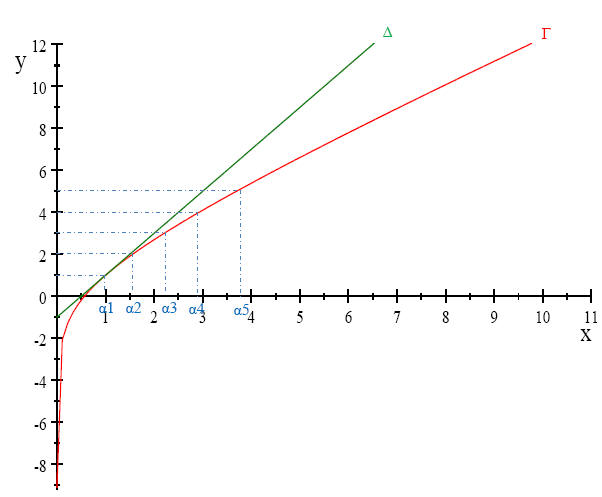
c)
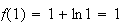
Donc
est l'unique solution de l'équation
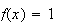
Donc
.
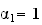d)
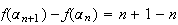
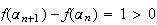
Or
la fonction f est strictement croissante sur
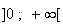
Donc
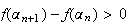implique
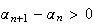
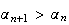
La
suite
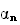est
donc strictement croissante
3)a)
Une équation de
,
tangente à
au
point A d'abcisse 1 s'écrit :
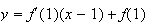
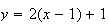
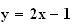
b)
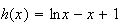
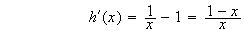
Le
signe de h'(x) dépend uniquement du signe de
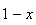car le dénominateur x est toujours positif.
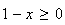quand
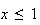
La
fonction est donc croissante sur
![$]0~;~1]$](graphics/HVRGOX83.png)
,
puis décroissante sur
.
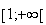Elle
présente donc un maximum pour
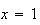qui vaut
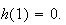
La
fonction h est donc négative sur
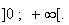
Position
relative de
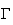par
rapport à
:
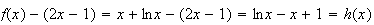
Or
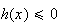pour tout x >0
Donc
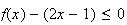
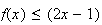
La
courbe
est
donc en dessous de
pour
tout réel positif.
c) Voir figure précédente
4)
On a vu à la question 3)b) que, pour tout x
>0,
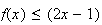
On
prend
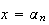
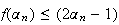
Or
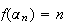par définition
Donc
.
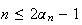
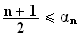Limite
de
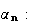
On
a
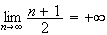
Donc par comparaison :
.
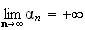PartieB :
1)
Soit
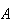un réel fixé
La
suite
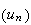étant non majorée, il existe un naturel
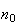tel que
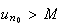
Par
croissance de la suite
.
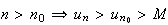Cette
propriété étant vraie pour tout réel
,
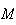la suite
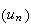tend vers
.
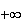Donc
un suite croissante non majorée tend vers
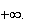
2)
Pour montrer que la suite
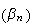n'est pas majorée, on raisonne par l'absurde :
On
suppose que la suite
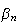est majorée.
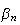étant croissante et majorée, elle converge.Appelons l sa limite.
g
étant continue,
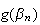converge vers g(l)
Or
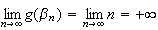
Contradiction
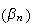n'est donc pas majorée.
De
plus
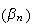est croissante
Donc
d'après la question précédente, la suite
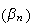tend
vers plus l'infini.
