CORRIGE de Mathématiques
Inde - Section S - Juin 2005
1)a)
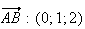et
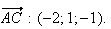Les
vecteurs
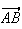et
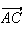ne
sont donc pas colinéaires
Donc A, B et C ne sont pas alignés.
b)
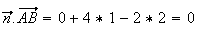
Donc
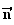est
orthogonal à
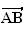
De
plus
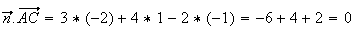
Donc
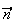est orthogonal à
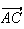
Conclusion
:
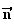est
orthogonal au plan (ABC) .
Détermination d'une équation cartésienne du plan (ABC) :
Le
plan ABC est donc le plan passant par A et orthogonal au vecteur
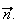
C'est
donc l'ensemble des points M(x;y;z) tels que
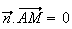
Soit
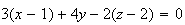
Soit
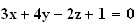
3)
Le vecteur
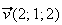est un vecteur orthogonal du plan
P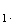
Le
vecteur
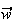(1;-2;6)
est un vecteur orthogonal du plan
P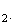
Ces
vecteurs ne sont pas colinéaires car il n'existe aucun k réél
tel que
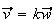ou
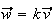
car
pour avoir l'égalité des abcisses on devrait avoir k=2 ou
k=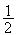
et l'égalité des ordonnées ne sont pas alors
vérifiées,
donc les plans P1 et P2 sont sécants, leur intersections est une droite.
Déterminons maintenant une équation cartésienne de cette droite.
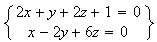
Si on soustrait à l'équation 1 , 2 fois l'équation 2.et on obtient :
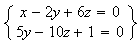
Posons
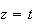avec t
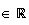
Le système devient :
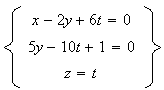
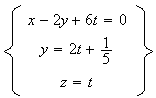
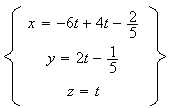
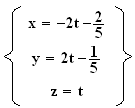
b)Par l'absurde, on va démontrer que D est parralèle au plan (ABC)
D est sécant au plan (ABC) si :
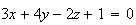
avec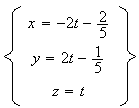
d'où
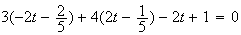
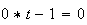
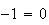
Impossible, cette équation n'a pas de solutions.
Donc la droite D est parallèle au plan (ABC).
3)a)
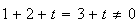car
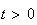
Donc le point G existe car la somme de ses coefficients est non nulle.
Soit I barycentre des points A et B affectés des coefficients 1 et 2.
I existe car la somme des coefficients est non nulle.
Les
coordonnées du point I sont
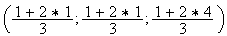soit
I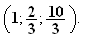
Expression
du vecteur
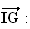
Le
point G est le barycentre de
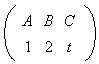donc le barycentre de
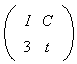donc :
(3+t)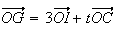
(3+t)(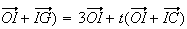
(3+t)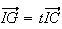
Or
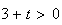
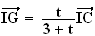
b) On cherche l'ensemble des points G lorsque t décrit l'ensemble des nombres réels positifs ou nuls.
Pour
cela, étudions les variations de
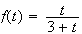sur
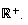
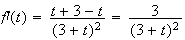
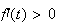
Donc f est strictement croissante.
De
plus
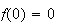
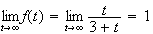
f
est donc continue, strictement croissante sur
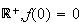et
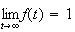donc l'image de
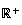par
f
est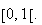
Le point G décrit donc le segment [IC] privé du point C.
Le point G est confondu avec J si et seulement si :
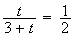soit
