CORRIGE de Mathématiques
Inde - Section S - Juin 2005
1)
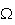est le milieu du segment [AB], diamètre du cercle C. Donc:
z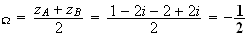
Le
rayon du cercle C est
[![$\Omega A]:$](graphics/JE2OIC2D.png)
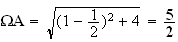
2)
Expresion algébrique de
z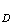
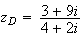
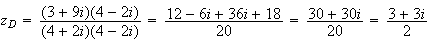
Pour
montrer maintenant que D est un point du cercle C, il
faut montrer que
D
est égale au rayon du cercle C soit
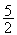
Calculons
donc
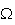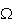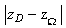
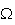D
:
D=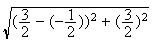
D=
D=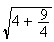
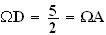
Donc D appartient au cercle C.
3)a)
Module de
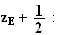
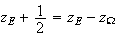
Donc
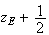est l'affixe de
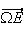
De plus E appartient au cercle de centre C.
Donc
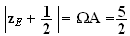
Argument
de
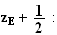
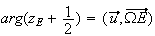
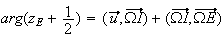d'après Chasles.
Or
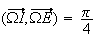et
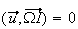
Donc
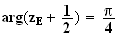à
2
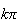près.
b)
D'après la question précédente , on peut écrire
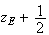sous la forme :
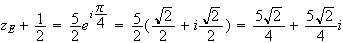
d'où
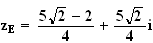
4)a) on sait que M' image de M par la transformation r a pour affixe z' telle que :
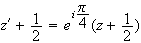
soit
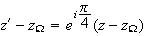
Donc
M' est l'image de M par la rotation de centre
et d'angle
b) K' est l'image de K par r. Donc :
'
'
'
'
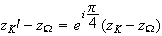
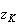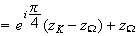
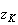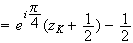
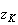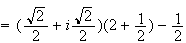
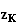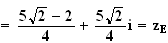
Donc K'=E
Géométriquement
K est un point du cercle C de centre
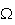car
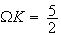(faire le calcul)
Donc son image par la rotation r sera un point de C et :
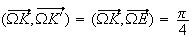
donc K'=E
