CORRIGE de Mathématiques
Inde - Section S - Juin 2005
1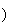
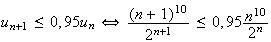
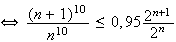
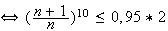
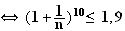
2)a)
Pour tout x
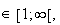on a :
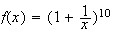
Calculons sa dérivée :
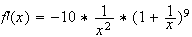
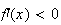
Donc
f est décroissante sur
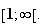
Limite
de f en
+
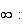
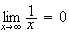
Donc
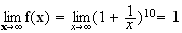
b)
f est continue, strictement décroissante sur
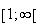
De
plus
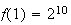
et
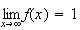
Le
réel 1,9 appartient à l'intervalle
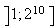
Donc
ce réel a un et un seul antécédent
.
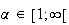Donc
il existe un unique réel
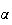
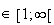tel que
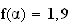
c)
On cherche
n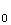
entier naturel tel que
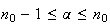
Avec
la calculatrice en résolvant
f(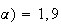
on trouve que
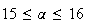
Donc
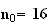
d)
La fonction f est décroissante sur
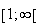et
f(
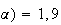
Or
si
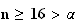
Alors
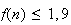soit
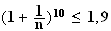
3)a)
D'après la question précédente, on a pour
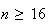
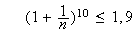
De
plus d'après la question 1, on a
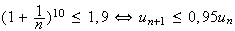
soit
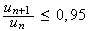
soit
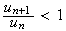
soit
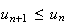
Donc
la suite
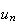est décroissante à partir du rang 16.
4)
Montrons par récurrence que pour tout n
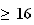on a 0
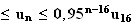
n=16 :
On
a bien 0
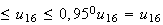
OK
n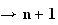
:
Pour
n >16 on a
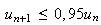
Or
d'après l'hypothèse de récurrence
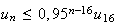
Donc
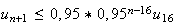
Soit
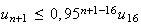
De
plus il est évident que
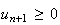
Finalement
on a 0
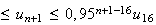
Conclusion :
Pour
tout n
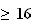on a 0
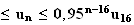
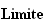de
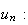
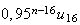est une suite géométrique de raison 0,95. Sa raison est
inférieur à 1 donc cette suite converge vers 0.
D 'après le théorème des gendarmes on en déduit que :
