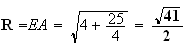Partie A :
Soit M un point de l'espace équidistants de K et L
On a pour tout point M :
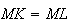
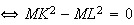
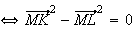
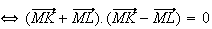
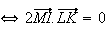car I milieu de MK + relation de chasles
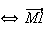est orthogonal à
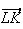
M appartient au plan médiateur de [KL]
Partie B :
1) Soit M un point de l'espace d'affixe (x ; y ; z)
Soit I le milieu de [AB].
Le
point
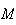appartient au plan médiateur de [AB] si et seulement si
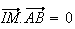
Or
I a pour coordonnée
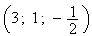
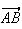a pour coordonée
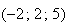
Donc
.
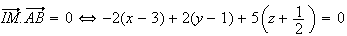
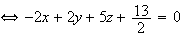
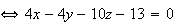Une
équation cartésienne du plan médiateur de [AB] est donc :
.
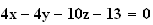2) Les coordonnées du point commun aux trois plans vérifient le système suivant :
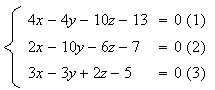
On
multiplie l'équation (1) par 3 et on l'ajoute à l'équation (3)
multipliée par
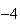. Ainsi
on obtient :
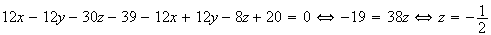
Le système devient alors :
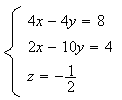
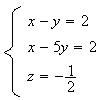
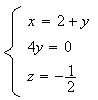
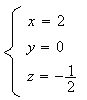
Les
trois plans médiateurs se coupent donc en un unique point E de
coordonée (2 ; 0 ;
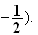
3) D'après la partie A :
EA = EB puisque E appartient au plan médiateur de [AB] ;
EB = EC puisque E appartient au plan médiateur de [BC] ;
EC = ED puisque E appartient au plan médiateur de [CD] ;
Donc EA = EB = EC = ED.
Les points A, B, C et D appartiennent donc à une même sphère de centre E et de rayon R
avec
