1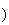 a)
L'affixe de E' est :
a)
L'affixe de E' est :
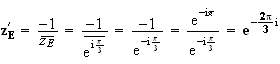
Expression
de
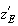 sous forme algébrique :
sous forme algébrique :
On
sait que
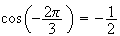 et
et
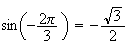
Donc
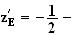 i
i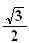
b) Soit M d'affixe z
M
appartient au cercle
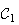 de
centre O et de rayon
1
de
centre O et de rayon
1 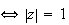

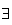
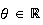 tel que :
tel que :
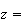 e
e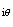
L'affixe de son image M' par f est donc :
z'=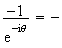 e
e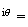 e
e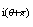
Donc
F(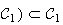
De
plus lorsque M décrit
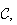
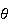 décrit
décrit
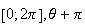 décrit
décrit
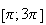 qui est inclus dans
qui est inclus dans
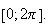
Donc
M' décrit
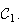
Donc
F(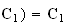
2)a)
L'affixe de
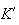 est :
est :
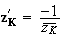
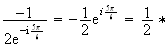 e
e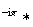 e
e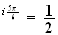 e
e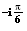
b) Soit M d'affixe z
M
appartient au cercle
 de
centre O et de rayon
2
de
centre O et de rayon
2 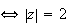

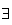
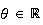 tel que :
tel que :
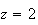 e
e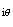
L'affixe de son image M' par F est donc :
z'=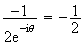 e
e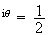 e
e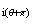
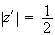
Donc
M' appartient au cercle
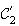 de centre O et de rayon
de centre O et de rayon
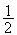
Donc
F(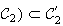
On
montre ensuite comme dans la question 1)a) que lorsque M décrit
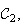 M' décrit
M' décrit
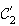 .
.
Donc
F(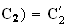
3)a)
On a
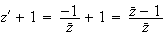 .
(On supose que
.
(On supose que
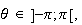 donc
e
donc
e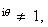 donc
donc
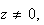 donc
donc
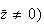
On
peut donc en déduire , en passant au module et en remplaçant z
par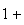 e
e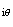 ,
dans l'expression précédente que :
,
dans l'expression précédente que :
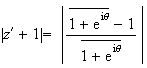 .
.
Or
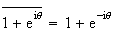
Donc
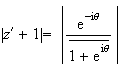
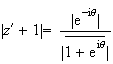
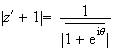
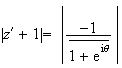
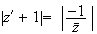
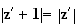
b)
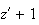 est l'affixe du vecteur
est l'affixe du vecteur
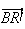
z'
est l'affixe du vecteur
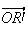
D'après
la question 3)a), on a
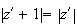
Donc BR'=OR'
Le point R' appartient donc à la médiatrice du segment [OB]
Les
images par F des points d'affixes
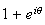 avec
avec
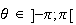 appartiennent donc à la médiatrice du segment [OB].
appartiennent donc à la médiatrice du segment [OB].

