1)
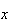
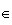
![$[0;1]$](graphics/HVNNBA9X.png)
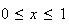
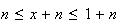
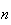
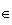
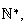 donc
donc
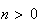 et
et
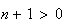
Ainsi en passant à l'inverse dans l'inégalité précédente, on obtient :
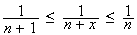
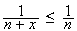
ce qui montre la première inégalité.
Démontrons
maintenant que
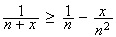 autrement dit que
autrement dit que
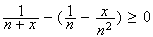
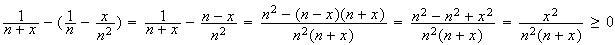
Donc
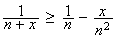
Finalement :
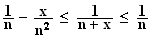
2)a)
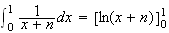 car
car
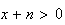
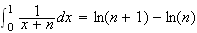
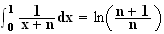
b) D'après 1, on a :
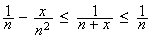
En passant à l'intégrale dans cette inégalité, on obtient :
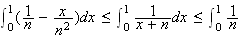 d
d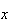
Or
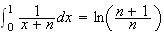 (d'après 2a))
(d'après 2a))
D'où :
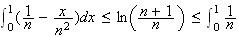 d
d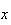
Or
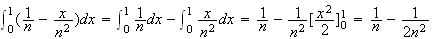
et
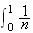 d
d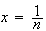
Donc :
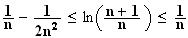
3)
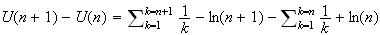
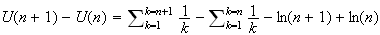
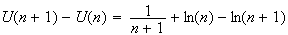 (somme télescopique)
(somme télescopique)
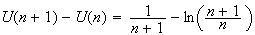
Or
d'après 2)b),
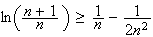
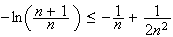
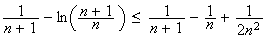
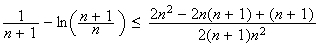
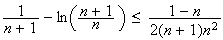
Or
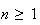
Donc
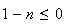
Donc
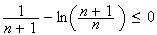
Donc
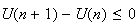
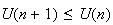
Donc
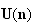 est décroissante.
est décroissante.
4)
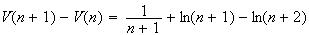
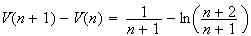
Or
d'après 2. b. en remplaçant
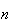 par
par
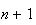 ,
on obtient que
,
on obtient que
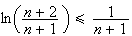 .
.
Donc
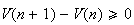 :
:
La
suite
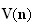 est donc croissante.
est donc croissante.
5)
D'après la question 4 et 3 ,
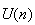 est décroissante et
est décroissante et
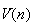 est croissante.
est croissante.
De
plus
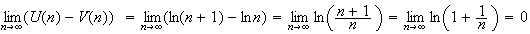 (car
(car
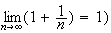
On
peut donc en déduire que les suites
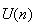 et
et
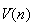 sont adjacentes. Elles sont donc convergentes et convergent vers la même
limite
sont adjacentes. Elles sont donc convergentes et convergent vers la même
limite
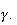
Valeur
approchée de
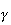 à
10
à
10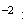
Les
suites étant adjacentes on a pour tout n
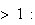
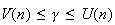
On
cherche n tel que
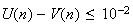
soit
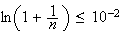
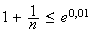
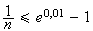
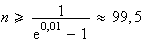
On prend donc n=100
A la calculatrice , on détermine :
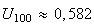 et
et
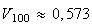
D'où
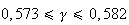
On en déduit que :
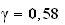 à
à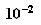 près
près

