CORRIGE MATHEMATIQUES FRANCE METROPOLITAINE
SECTION S - Juin 2001
Partie A :
1.
Pout tout x
:
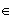
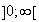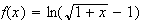
limite de f en 0 :
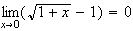
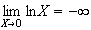
donc :
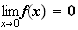
limite
de f en
+
:
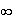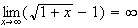
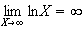
donc :
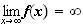
2.
Sens de variation de f sur
:
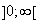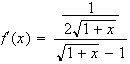
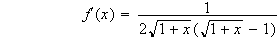
x étant positif
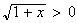
et
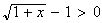
Donc pour tout x >0
f'(x) > 0
Tableau de variation de f :
____________________________________________
x 0 +
____________________________________________
+
____________________________________________
-
+
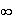
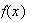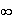
3.
L'ordonnée
y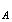
de A s'écrit :
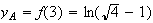
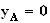
L'ordonnée
y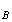
de B s'écrit :
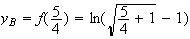
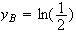
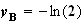
P
est le projeté orthogonal de B de coordonées
(
)
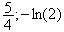sur l'axe
(O,
).
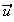Donc
par définition du projeté, P a pour coordonnées
(
)
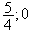dans le repère
(O,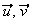
).
H est
le projetéorthogonal de B sur
(O,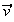
).
Donc
H a pour coordonnées
(
)
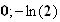PARTIE B :
1.a)
La rotation de centre O et d'angle
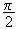transforme M d'affixe z en M' d'affixe z' .
Donc:
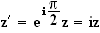
Si z=x+iy et z'=x'+iy'avec x, y ,x',y' rééls
On obtient la relation suivante :
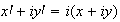
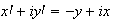
En égalant parties imaginaires et parties réelles , on obtient:
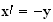
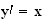
b) A' image de A (3 ; 0) par la rotation r. Donc d'aprés la question précédente A' a pour coordonnées (0 ; 3).
B'
image de B
(
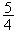; -ln2) par la rotation r. Donc d'aprés la question précédente
B' a pour coordonnées (ln2
;
).
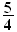P'
image de P
(
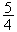; 0) par la rotation r. Donc d'aprés la question précédente
B' a pour coordonnées (0
;
)
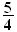2. M(x ; y) appartient à (C).SSI y=f(x)où x > 0
Son
image M' par r admet pour coordonnées (x' ; y') avec
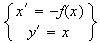
Nous
avons montré à la partie A question 2 que f décrit
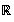lorsque x décrit
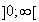
De plus , on a :
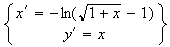
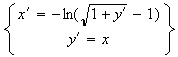
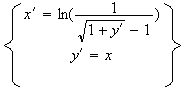
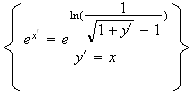
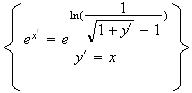
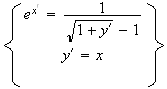
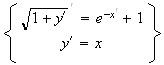
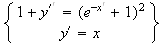
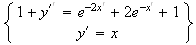
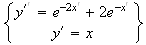
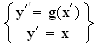
Donc
si M appartient à (C) , son image M' appartient à
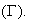
c) représentation graphique :
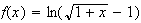
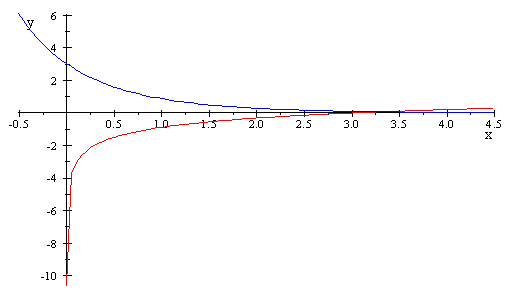
PARTIE C :
1)
Soit
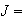
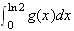
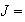
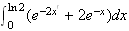
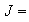
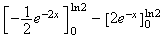
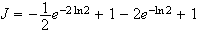
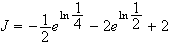
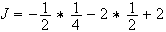
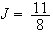
g
est la somme de deux fonctions positives sur
(
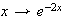et
)
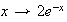Donc
g est positive sur
Par
conséquent J représente l'aire exprimée en unitée
d'aire du domaine plan (D') délimité par
,
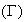l'axe des abcisses, l'axe des ordonnées et la droite d'équation
y=ln2
2.a)On
a g(0)=3 ; I représente l'aire du domaine délimité par [A'O],
[HO'] et [H'B'] et l'arc de courbe
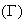d'extrémité A' et B'.
Or O, A', H', B' sont les images respectives de O,A, H et B par la rotation r .
Donc (D') est l'image de (D) par la rotation r.
Or la rotation conserve les aires, on peut donc en déduire que (D) et (D') ont la même aire.
Ainsi
A=J=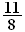
b)
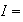
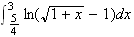
On a A= aire (OPBH) + I
d'où
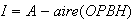
Or
OPBH est un rectangle de cotés
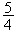et
ln2 ; donc son aire en unité d'aire est égale à (
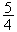ln2
)unité d'aire
d'où
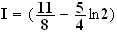unité d'aire
soit
I
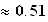unité d'aire
