CORRIGE MATHEMATIQUES FRANCE METROPOLITAINE
SECTION S - Juin 2001
1.
Pour tout n
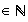 :
:
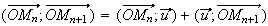
![$\ [2\pi ]$](graphics/J9B4RIH1.png)
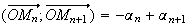
![$[2\pi ]$](graphics/J9B4RIH5.png)
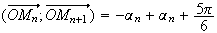
![$[2\pi ]$](graphics/J9B4RIH9.png)
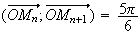
![$[2\pi ]$](graphics/J9B4RIHD.png)
On
peut en déduire que puisque
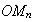
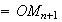 (M et N appartiennent au même cercle de centre O )
(M et N appartiennent au même cercle de centre O )
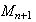 est
l'image de
est
l'image de
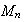 par la rotation de centre O et d'angle
par la rotation de centre O et d'angle
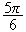 .
.
Ce calcul préliminaire nous permet de placer les 12 points sur le graphique ci dessous (voir fichier autre logiciel) :
2.
M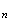 d'affixe
z
d'affixe
z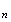 appartient au cercle C de centre O et de rayon 1 tel que l'angle
appartient au cercle C de centre O et de rayon 1 tel que l'angle
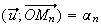
Donc
z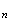 s'écrit :
s'écrit :
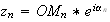
Le
cercle C a un rayon de
1 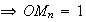
De
plus
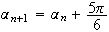
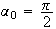
Donc
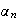 est suite arithmétique de raison
est suite arithmétique de raison
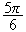
On
peut donc écrire
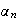 de la façon suivante :
de la façon suivante :
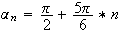
d'où :
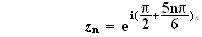
3.
M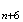 a pour abcisse :
a pour abcisse :
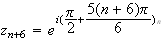
z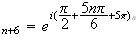
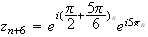
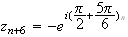
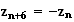
Les
points
M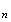 et
M
et
M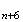 sont
donc diametralement opposés .
sont
donc diametralement opposés .
M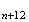 a pour abcisse :
a pour abcisse :
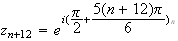
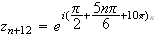
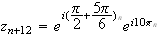
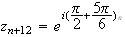
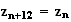
Les
points
M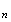 et
M
et
M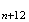 sont
donc cofondus .
sont
donc cofondus .
b)Pour
tout
n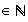 ,
on a :
,
on a :
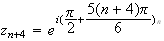
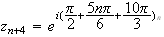
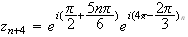
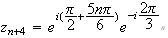
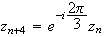
Calculons
maintenant la distance
M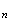 M
M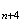 :
:
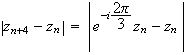
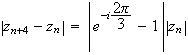
Or
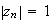 car
M
car
M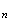 appartient au cercle trigonométrique .
appartient au cercle trigonométrique .
D'où :
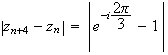
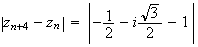
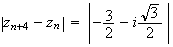
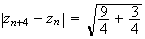
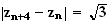
La
distance
M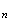 M
M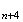 vaut
donc
vaut
donc
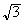 .
.
Montrons
maintenant que le triangle
M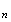 M
M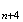 M
M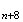 est un triangle équilatéral :
est un triangle équilatéral :
Le
centre du cercle circonscrit au triangle
M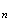 M
M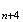 M
M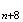 est O et la rotation d'angle
est O et la rotation d'angle
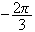 transforme
M
transforme
M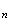 en
M
en
M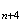 et
M
et
M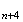 en
M
en
M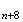 car
car
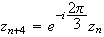 et
et
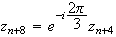
On
peut en déduire que le triangle
M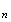 M
M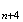 M
M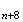 est
équilatéral.
est
équilatéral.
4.On
tire simultanémént 3 cartons de l'urne qui en contient 12. Il y a
donc
C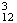 =
220 tirages successifs
=
220 tirages successifs
On
admet que tous les triangles équilatéraux sont de la forme
M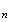 M
M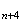 M
M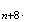
Il y a donc 4 cas possibles pour obtenir les trois sommets d'un triangle équilatéral.
Ils
correspondent aux triangles
M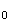 M
M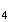 M
M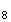 ,
M
,
M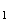 M
M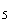 M
M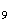 ,
M
,
M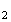 M
M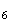 M
M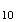 ,
M
,
M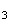 M
M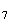 M
M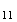 ,M
,M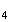 M
M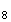 M
M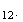
La
probalité d'obtenir les trois sommets d'un triangle équilatéral
est donc de
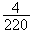 soit
soit
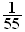 .
.

