1.a)Loi de probalité :
Les tirages des trois boules étant équiprobables, le nombre de triplets possibles est :
L'évenement [X=0] est l'évenement "tirer zéro boules rouges", donc tirer 3 boules vertes parmis les trois boules vertes d'où :
L'évenement [X=1] est l'évenement "tirer 1 boule rouge et 2 boules vertes", donc tirer 1 boule rouge parmi les 10 et 2 boules vertes parmis les trois boules vertes d'où :
De même on a :
b) Espérance mathématique de X :
2.a)
L'enfant a une chance sur 2 de choisir la boite cylindrique ou la
boite cubique car il la choisit au hasard. Donc
p(C1)=p(C2)=
Comme
il y a 3 boules vertes et 10 boules rouges dans la boite cubique , la
probalité de tirer des boules vertes sachant que l' enfant a choisi la
boite cubique est
p(C1/V)=
De
même la probalité de tirer des boules rouges sachant que l'enfant a
choisi la boite cubique est
Comme
il y a 4 boules vertes et 3 boules rouges dans la boite cylindrique, on a
et
D' où l' arbre pondéré des évenements
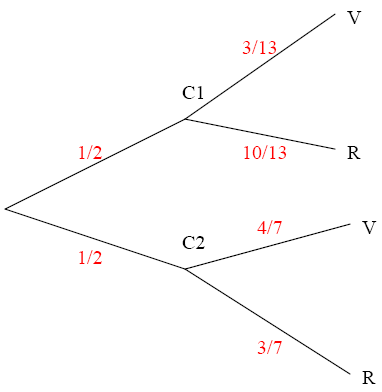
b) Les evènements C1 et C2 sont incompatibles donc R = (R∩C1) U (R∩C2)
(d'apres la formule des probalités totales)
c)
p(C1/R)
3.a) On cherche la probalité telle que l'enfant ait pris au moins une bille rouge au cours de ses n choix. Pour résoudre ce problème, on calcule la probalité de son évènement contraire c'est
à
dire la probalité de l'évenement "ne jamais prendre de bille rouge
aucours des n tirages. Cette probalité est :
d'ou
la probalité cherchée est :
b)
On cherche la plus petite valeur de n pour laquelle
≥ 0,99
On
a :
c'est à dire
soit
Donc
la plus petite valeur de n pour laquelle
est
6.
