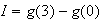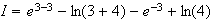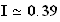Partie A :
1.
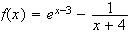
Calcul de la dérivée de f :
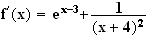
2.
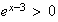 et
et
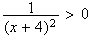 pour tout x
pour tout x
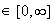
Donc
f'(x) > 0 pour tout x
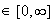
Donc
f est strictement croissante sur
![$[0,\infty ]$](graphics/J9CL568Z.png) .
.
3.
limite de f en
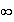 :
:
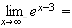
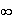 car
car
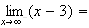
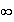 et
et
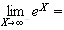
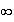
de plus :
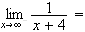
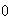
donc :
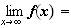
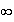
4.a) Tableau de variation de f :
____________________________________________
x
0+
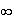
____________________________________________
 +
+
____________________________________________
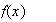
 +
+
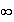
avec
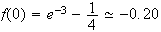
b)
Il existe
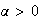 tel que
tel que
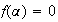
Sur l'intervalle [ 0;+∞ [ la fonction f est strictement croissante donc
Si
x <
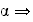
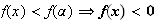
Si
x >
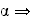
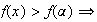
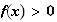
5)a)
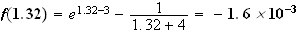
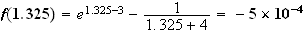
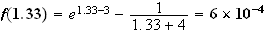
b)Sur
l'intervalle [ 0;+∞ [ , la fonction f est dérivable et strictement
croissante et
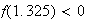 et
et
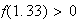
Donc
d'aprés le théorème des valeurs intermédiaires il existe un
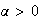 tel que
tel que
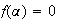
et
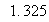
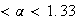
Donc
l'arrondi au centième de
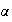 est
1.33
est
1.33
Partie B :
1)a)
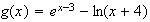
Calcul de la dérivée de g :
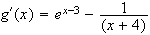
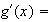
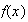
On
remarque que
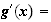
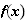
b)
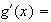
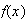
Donc le signe de g'(x) dépend du signe de f . Or d'après la question 4 à la partie A:
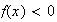 pour x <
pour x <
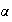
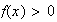 pour x >
pour x >
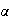
Donc :
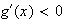 pour x <
pour x <
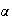
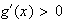 pour x >
pour x >
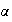
Donc :
g
est décroissante pour x <
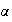
g
est croissante pour x <
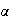
2) Calcul de I :
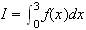
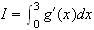 d'après question 1)a)
d'après question 1)a)