CORRIGE de Mathématiques
France Métropolitaine - Section ES - Juin 2003
Partie A
1.a.
Sur
![$[0,50]$](graphics/Bac_ES_France_Juin 2003_Maths_Corrige_Pb__1.png) ,
g est dérivable comme produit de fonctions dérivables et on a :
,
g est dérivable comme produit de fonctions dérivables et on a :
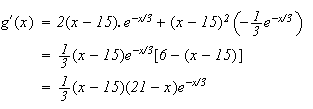
b.
Sur
![$[0,50]$](graphics/Bac_ES_France_Juin 2003_Maths_Corrige_Pb__3.png) ,
,
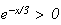 donc
donc
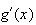 est du signe de
est du signe de
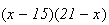
c.
2.
sur
![$[0,50]$](graphics/Bac_ES_France_Juin 2003_Maths_Corrige_Pb__9.png) ,
G est dérivable comme produit de fonctions usuelles dérivables et on
a :
,
G est dérivable comme produit de fonctions usuelles dérivables et on
a :
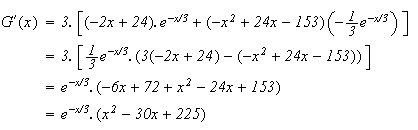
Or
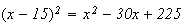
Donc
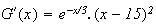
Donc
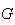 est une primitive de
est une primitive de
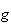 sur
sur
![$[0,50]$](graphics/Bac_ES_France_Juin 2003_Maths_Corrige_Pb__15.png)
Partie B
1.
Sur
![$[15,49]$](graphics/Bac_ES_France_Juin 2003_Maths_Corrige_Pb__16.png) on a :
on a :
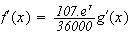 avec
avec
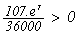
donc
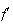 est
du même signe que
est
du même signe que
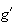 sur
sur
![$[15,49]$](graphics/Bac_ES_France_Juin 2003_Maths_Corrige_Pb__21.png)
donc
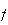 admet les mêmes variations que
admet les mêmes variations que
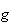 sur
sur
![$[15,49]$](graphics/Bac_ES_France_Juin 2003_Maths_Corrige_Pb__24.png)
2.
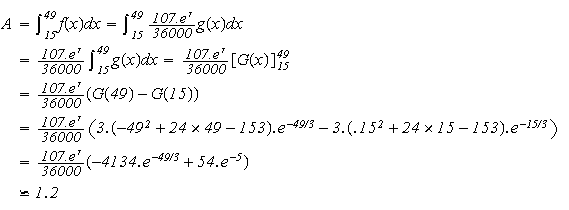
or
1unité d'aire :
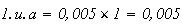
donc
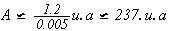
Partie C
1.
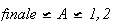
2.
En arrondissant à
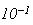 on trouve le même résultat
(
on trouve le même résultat
(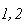 )
entre le modèle et la valeur théorique
)
entre le modèle et la valeur théorique
de la somme des taux de fécondité
Donc le modèle choisi paraît adapté
3.
Valeur moyenne de f sur
![$[15,49]$](graphics/Bac_ES_France_Juin 2003_Maths_Corrige_Pb__32.png) :
:
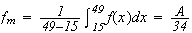
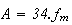
Donc
la descendance finale n'est pas égale à
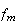 mais
à
mais
à