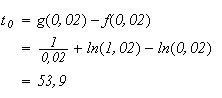Partie A
1.
Pour tout
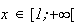

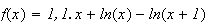
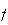 est dérivable comme somme de fonctions dérivables et on a :
est dérivable comme somme de fonctions dérivables et on a :
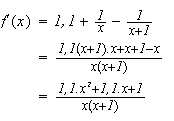
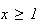 donc
donc
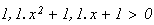 et
et
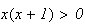
Pour
tout
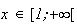

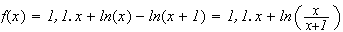
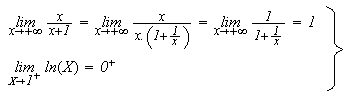 donc
donc
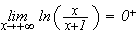
De
plus
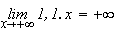
Donc
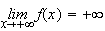
2.
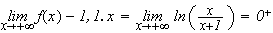 (d'après la question 1.)
(d'après la question 1.)
Donc
la droite d'équation
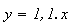 est une asymptote de la courbe
est une asymptote de la courbe
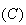
Soit
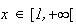 , on a
, on a
 :
:
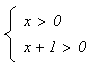 donc
donc
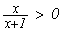
On
a aussi
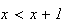
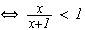 car
car
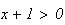
Donc
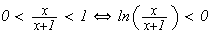
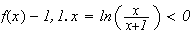 : donc l'aymptote
: donc l'aymptote
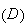 est
au dessus de la courbe
est
au dessus de la courbe
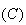
3.
Partie B
1.
Sur
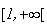 ,
,
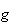 est dérivable comme somme de fonctions dérivables et on a :
est dérivable comme somme de fonctions dérivables et on a :

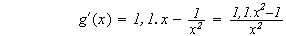
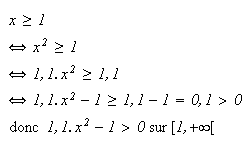
Or
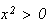 sur
sur
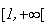 , donc
, donc
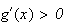 sur
sur
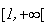
Donc
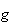 est strictement croissante sur
est strictement croissante sur
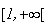
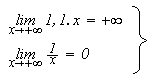 donc
donc
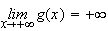
2.
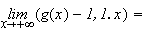
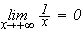
Donc
 est une asymptote de la courbe
est une asymptote de la courbe
 en
en
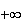
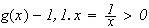 car
car
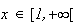
donc
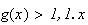 c'est à dire que la courbe
c'est à dire que la courbe
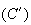 est au dessus de la courbe
est au dessus de la courbe
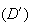
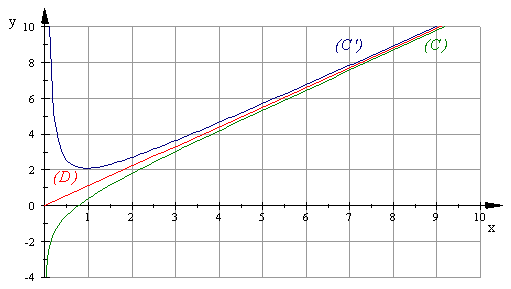
3. (Voir le graphique)
4.
Sur
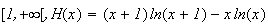 :
:
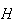 est dérivable comme somme de fonctions dérivables
est dérivable comme somme de fonctions dérivables
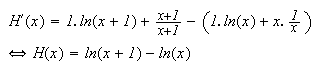
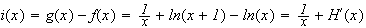
Une
primitive de
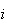 sur
sur
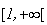 :
:
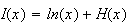
5.
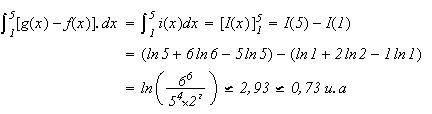
Cette
intégrale correspond à l'aire comprise entre la courbe
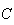 ,
la courbe
,
la courbe
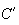 et les droites d'équations
et les droites d'équations
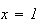 et
et
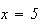
Partie C
1. Pour
tout
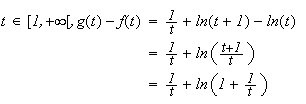
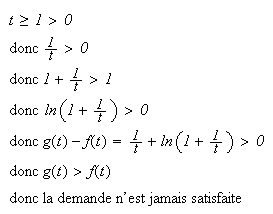
2.
D'après la question B.5 , on a :
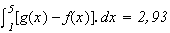
Donc le nombre total d'objet dont la demande n'est pas satisfaite entre les dates 1 et 5 est de 3
3.
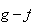 est décroissante sur
est décroissante sur
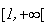
Donc
le niveau de fabrication est suffisant à partir de la date